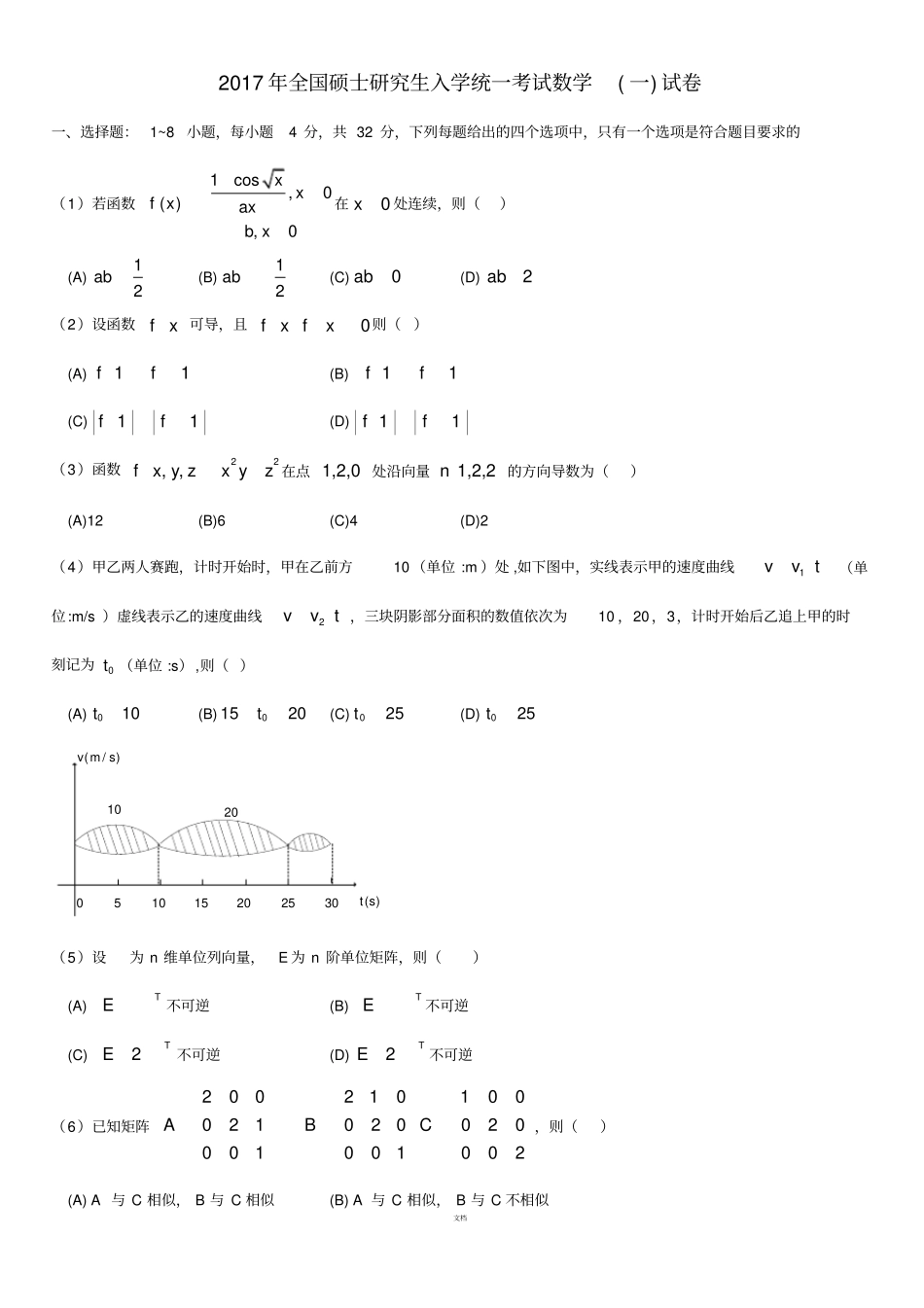
文档2017 年全国硕士研究生入学统一考试数学( 一) 试卷一、选择题: 1~8小题,每小题4 分,共 32 分,下列每题给出的四个选项中,只有一个选项是符合题目要求的(1)若函数1cos,0( ),0x xf xaxb x在0x处连续,则()(A)12ab(B)12ab(C)0ab(D)2ab(2)设函数fx 可导,且0fx fx则()(A)11ff(B) 11ff(C)11ff(D)11ff(3)函数22, ,fx y zx yz 在点 1,2,0 处沿向量1,2,2n的方向导数为()(A)12 (B)6 (C)4 (D)2 (4)甲乙两人赛跑,计时开始时,甲在乙前方10 (单位 :m )处 ,如下图中,实线表示甲的速度曲线1vvt(单位:m/s )虚线表示乙的速度曲线2vvt ,三块阴影部分面积的数值依次为10 ,20 ,3,计时开始后乙追上甲的时刻记为0t (单位 :s),则( )(A)010t(B)01520t (C)025t(D)025t051015202530( )t s(/ )v m s1020(5)设为 n 维单位列向量,E 为 n 阶单位矩阵,则()(A) TE不可逆(B) TE不可逆(C) 2TE不可逆(D)2TE不可逆(6)已知矩阵200021001A210020001B100020002C,则()(A) A 与 C 相似, B 与 C 相似(B) A 与 C 相似, B 与 C 不相似文档(C) A 与 C 不相似, B 与 C 相似(D) A 与 C 不相似, B 与 C 不相似(7)设,A B 为随机事件,若0( )1,0( )1P AP B,则 P A BP A B 的充分必要条件是()A. P B AP B AB P B AP B AC. PPB AB AD. PPB AB A(8 )设12,......(2)nXXXn来自总体(,1)N的简单随机样本, 记11niiXXn则下列结论中不正确的是:()(A) 2()iX服从2 分布(B) 212()nXX服从2 分布(C) 21()niiXX服从2 分布(D) 2()n X服从2 分布二、填空题: 9~14小题,每小题4 分,共 24 分。(9) 已知函数21( )1f xx,则(3) (0)f__________ (10 )微分方程230yyy的通解为 y__________ (11 )若曲线积分Lyxdydyxdx122在区域22D,1x yxy内与路径无关,则a(12 )幂级数1111nnnnx在区间( -1,1 )内的和函数( )S x(13 )设矩阵101112011A,123,,为线性无关的3 维列向量组,则向量组123,,AAA的秩为(14 )设随机变量X 的分布函数为40.50.52xFxx,其中x 为标准正态分布函数,则EX= 三、解答题: 15~23小题,共 94 分。解答应写出文字说明、证明过程或演算步骤。(15 )(本题满分10 分)设函数,f u v 具有 2 阶连续偏导数,,xyf ecosx ,求0dydxx,220ddxyx(16 )(本题满分10 分)文...