应力强度因子

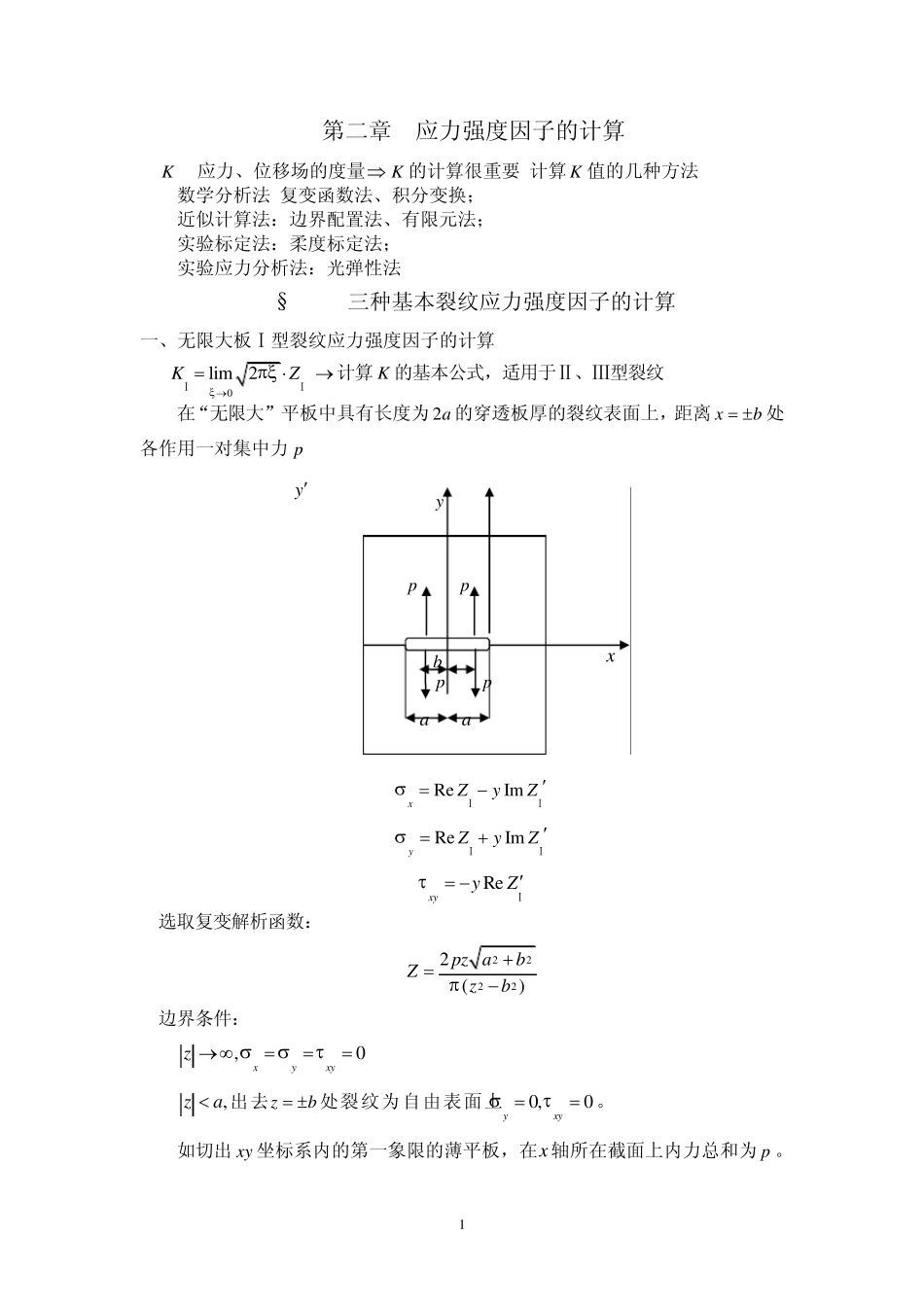
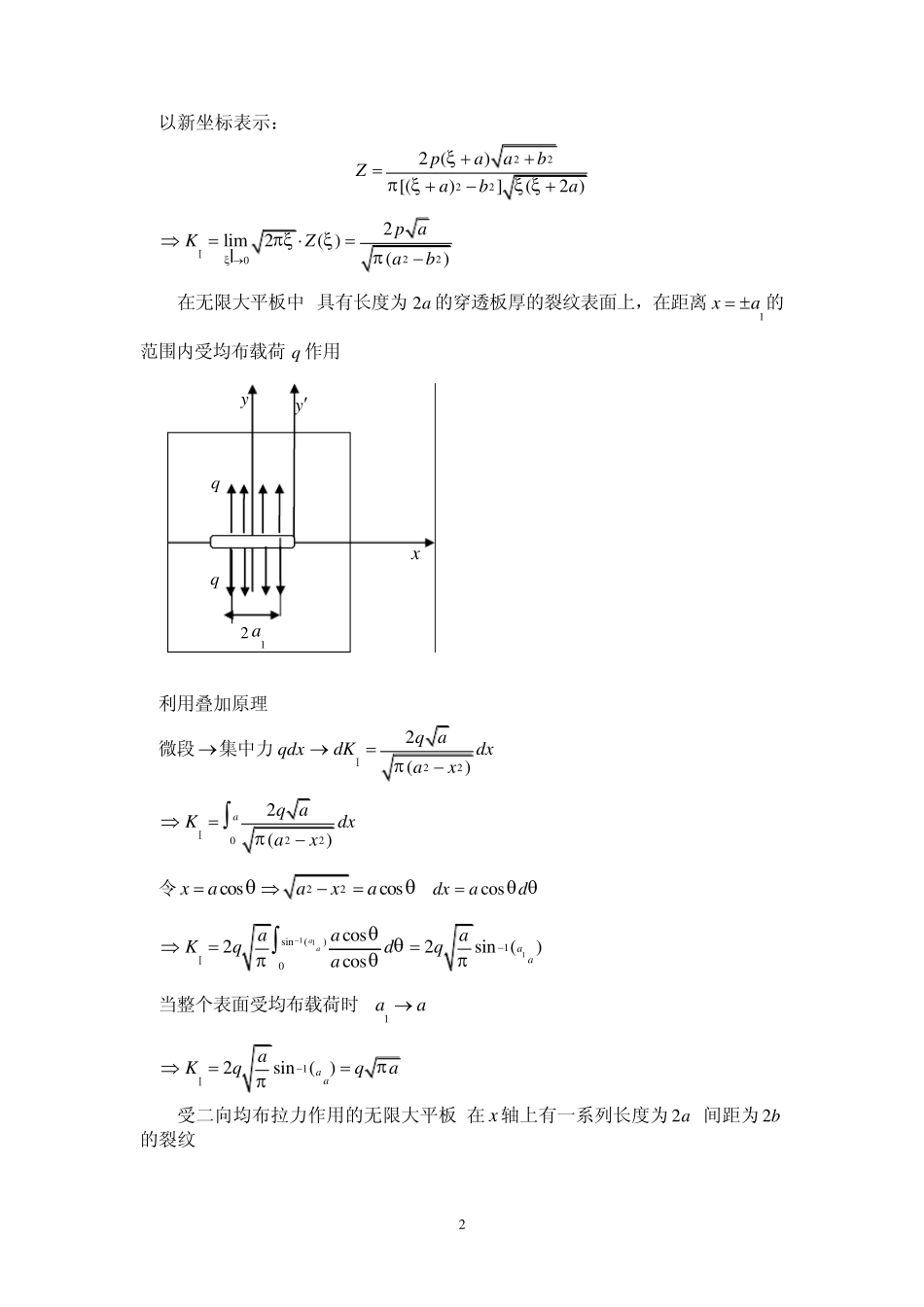
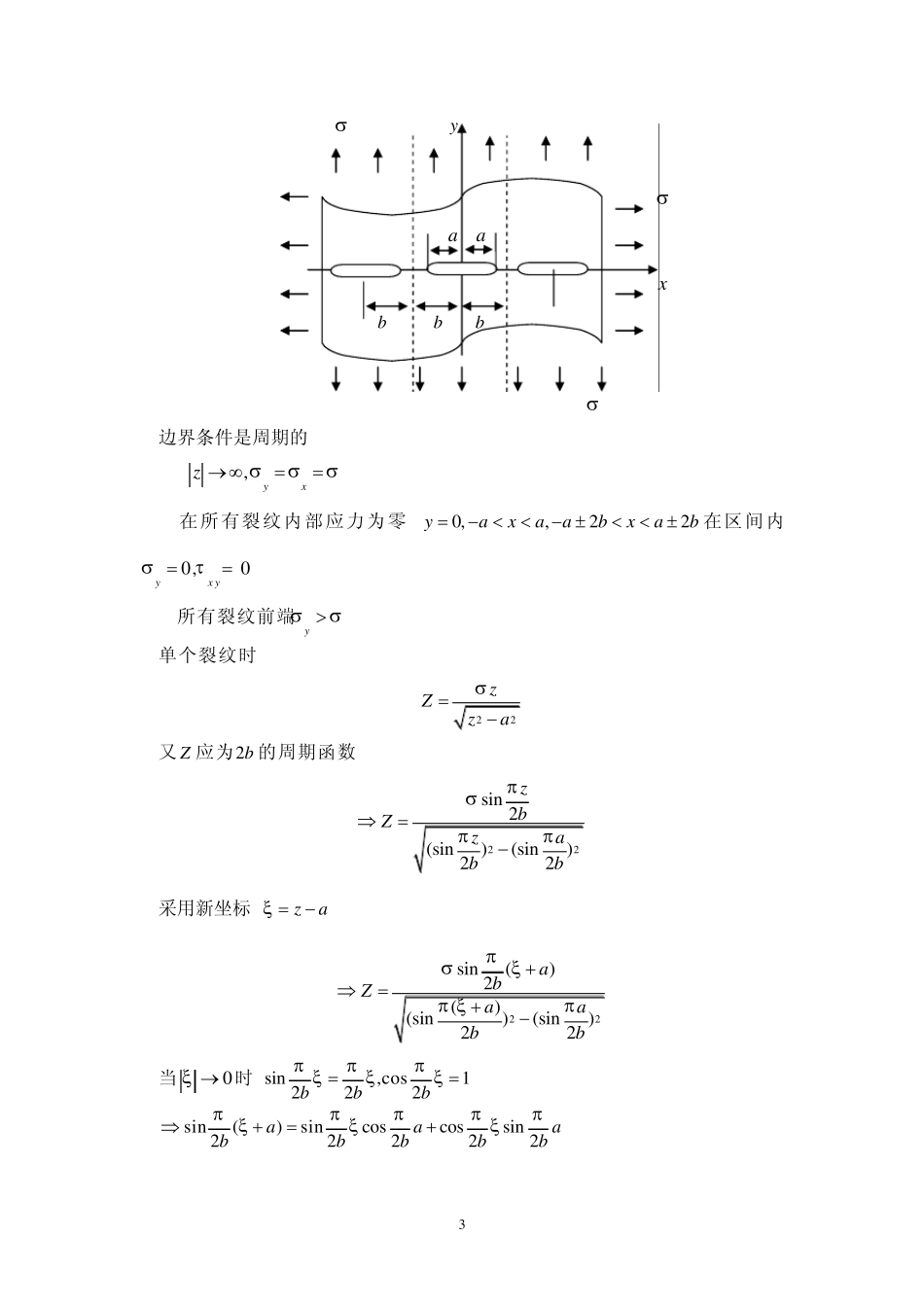
1 第二章 应力强度因子的计算 K --应力、位移场的度量 K 的计算很重要,计算K 值的几种方法: 1.数学分析法:复变函数法、积分变换； 2.近似计算法：边界配置法、有限元法； 3.实验标定法：柔度标定法； 4.实验应力分析法：光弹性法. §2-1 三种基本裂纹应力强度因子的计算 一、无限大板Ⅰ型裂纹应力强度因子的计算 0lim2KZⅠⅠ计算K 的基本公式，适用于Ⅱ、Ⅲ型裂纹 . 1.在“无限大”平板中具有长度为 2a 的穿透板厚的裂纹表面上，距离 xb  处各作用一对集中力p . ReImxZyZⅠⅠ ReImyZyZⅠⅠ RexyyZ Ⅰ 选取复变解析函数： 22222()pz abZzb 边界条件： a.,0xyxyz. b.,za出去zb  处裂纹为自由表面上0,0yxy。 c.如切出 xy 坐标系内的第一象限的薄平板，在x 轴所在截面上内力总和为 p 。 p p p p a a b x y y 2 以新坐标表示： 22222 ()[()](2 )paabZaba   2202lim2( )()p aKZabⅠ 2.在无限大平板中,具有长度为 2a 的穿透板厚的裂纹表面上，在距离1xa 的范围内受均布载荷 q 作用. 利用叠加原理: 微段 集中力 qdx 222()q adKdxaxⅠ 2202()aq aKdxaxⅠ 令22coscosxaaxa,cosdxad  111sin()10cos22sin ()cosaaaaaaaKqdqa Ⅰ 当整个表面受均布载荷时 ,1aa. 12sin ( )a aaKqqaⅠ 3.受二向均布拉力作用的无限大平板,在 x轴上有一系列长度为 2a ,间距为 2b的裂纹. q q x y 21a y 3 边界条件是周期的: a. ,yxz. b.在所有裂纹内部应力为零.0,,22yaxaabxab  在区间内0,0yx y c.所有裂纹前端y 单个裂纹时 22zZza 又 Z 应为2b 的周期函数 22sin 2(sin)(sin)22zbZzabb 采用新坐标:za  22sin()2()(sin)(sin)22abZaabb  当0 时,sin,cos1222bbb  sin()sincoscossin22222aaabbbbb x a a    y b b b 4 cossin222aabbb 2222[sin()]() cos2cossin(sin)2222222aaaaabbbbbbb 22[sin()](sin)2cossin22222aaaab...