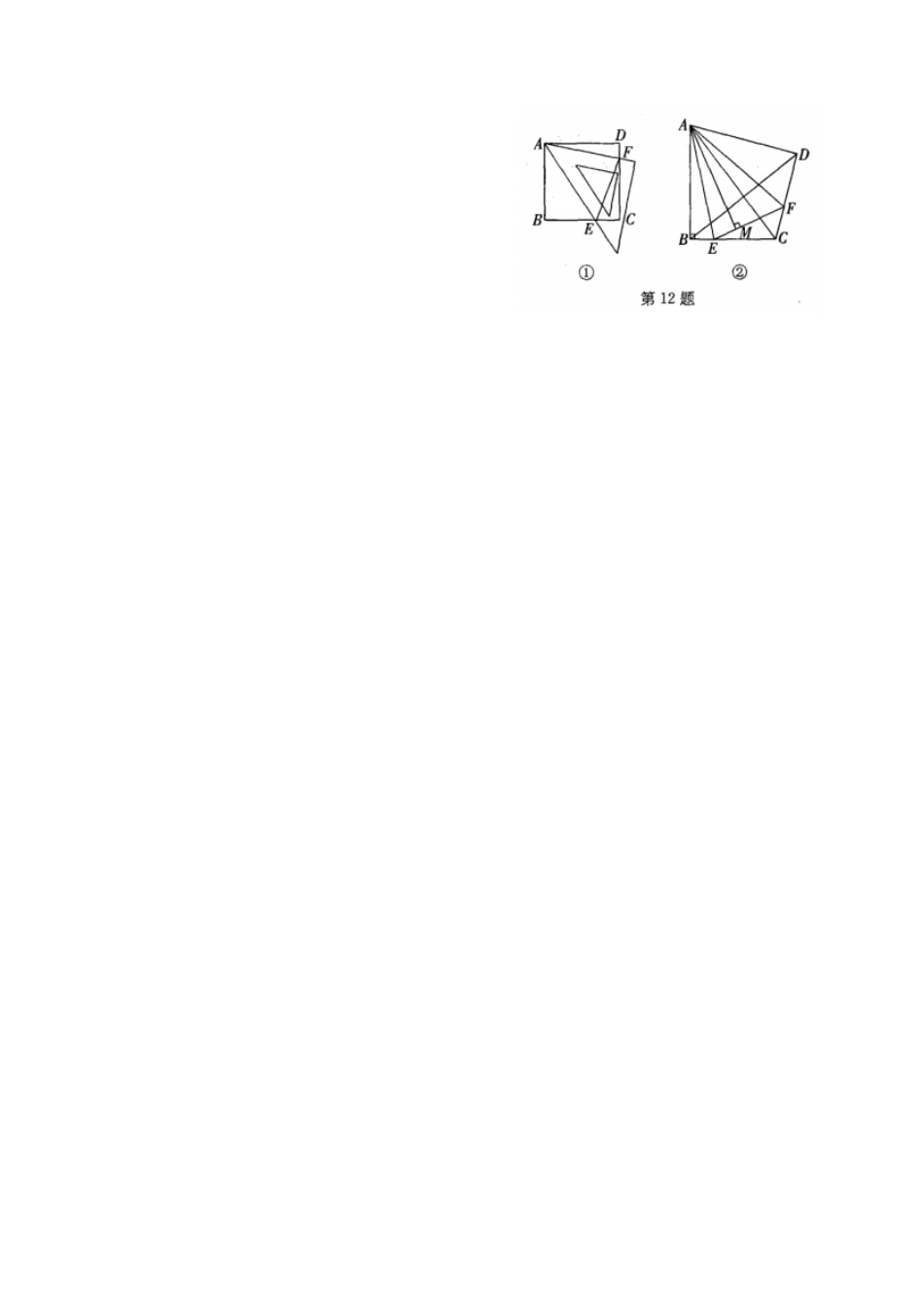
初中数学试卷灿若寒星整理制作矩形、菱形、正方形(5) 1.正方形具有而菱形不一定具有的性质是( ) A .对角线互相垂直B.对角线互相平分C.对角线相等D.对角线平分一组对角2.下列判断中正确的是( ) A .四边相等的四边形是正方形B.四角相等的四边形是正方形C.对角线互相垂直的平行四边形是正方形D.对角线互相垂直平分且相等的四边形是正方形3.如图,已知正方形ABCD 的边长为 3,E 为 CD 边上一点, DE=1.以点 A 为中心,把△ADE 顺时针旋转90° ,得△ ABE' ,连接 EE',则 EE'的长等于 _______.4.如图,过正方形ABCD 的顶点 B 作直线 l,过 A 、C 作 l 的垂线,垂足分别为E、F.若AE =1,CF= 3,则 AB 的长度为 _______.5.如图,三个边长均为2 的正方形重叠在一起,O1、O2 是其中两个正方形的中心,则阴影部分的面积是_______.6.如图,△ ABC 中, AB =AC,AD 是△ ABC 的角平分线,点O 为 AB 的中点,连接DO并延长到点E,使 OE= OD,连接 AE 、BE.(1)求证:四边形AEBD 是矩形;(2)当△ ABC 满足什么条件时,矩形AEBD 是正方形?并说明理由.7.已知四边形ABCD 中,∠ A =∠ B=∠ C=90° ,如果添加一个条件,即可推出该四边形是正方形,那么这个条件可以是( ) A .∠ D=90°B. AB =CD C.AD =BC D.BC=CD 8.如图所示, E、F 分别是正方形ABCD 的边 CD 、AD 上的点,且CE=DF,AE、BF 相交于点 O,下列结论① AE =BF;② AE ⊥BF;③ AO =OE;④S△AOB= S 四边形 DEOF 中,错误的有 ( ) A .1 个B.2 个C. 3 个D.4 个9.如图,在边长为2 的正方形 ABCD 中, M 为边 AD 的中点,延长MD 至点 E,使 ME=MC ,以 DE 为边作正方形DEFG ,点 G 在边 CD 上,则 DG 的长为( ) A .3 -1 B.3-5C.5 +1 D.5 -1 10.如图,在正方形ABCD 中, E 是 AB 上一点, BE=2,AE =3BE,P 是 AC 上一动点,则 PB+PE 的最小值是 _______.11.已知正方形ABCD ,以 CD 为边作等边△ CDE ,则∠ AED 的度数是 _______.12.如图①,等腰直角三角板的一个锐角顶点与正方形ABCD 的顶点 A 重合,将此三角板绕点 A 旋转,使三角板中该锐角的两条边分别交正方形的两边BC、DC 于点 E、F,连接 EF.(1)猜想 BE、EF、DF 三条线段之间的数量关系,并证明你的猜想;(2)在图①中,过点A 作 AM ⊥EF 于点 M ,请直接写出AM 和 AB 的数量关系;(3)如图②.将Rt△ABC 沿斜边 AC 翻折得到 Rt△ADC ,E、 F 分别是 BC、CD 边上的点,∠ EAF= 12∠BAD ,连接 EF,过点 A 作 AM ⊥EF 于点 M .试猜想 AM 与 AB 之间的数量关系,并证明你的猜想.参考答案1.C 2.D 3.204.105.2 6.略7.D8.A9.D 10. 10 11.15° 或75°12.(1) EF=BE+ DF.(2)AM =AB ;(3)AM =AB .