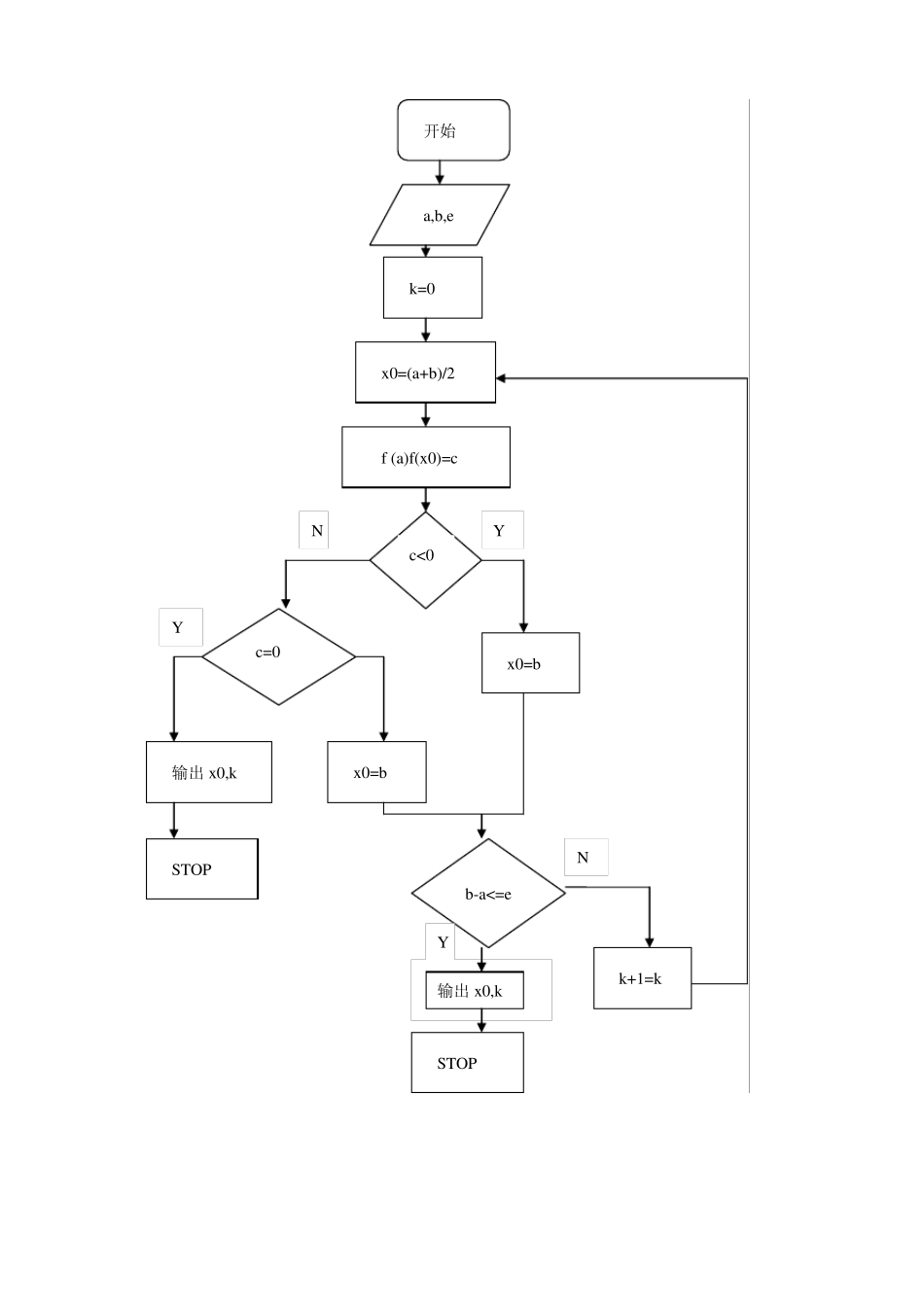
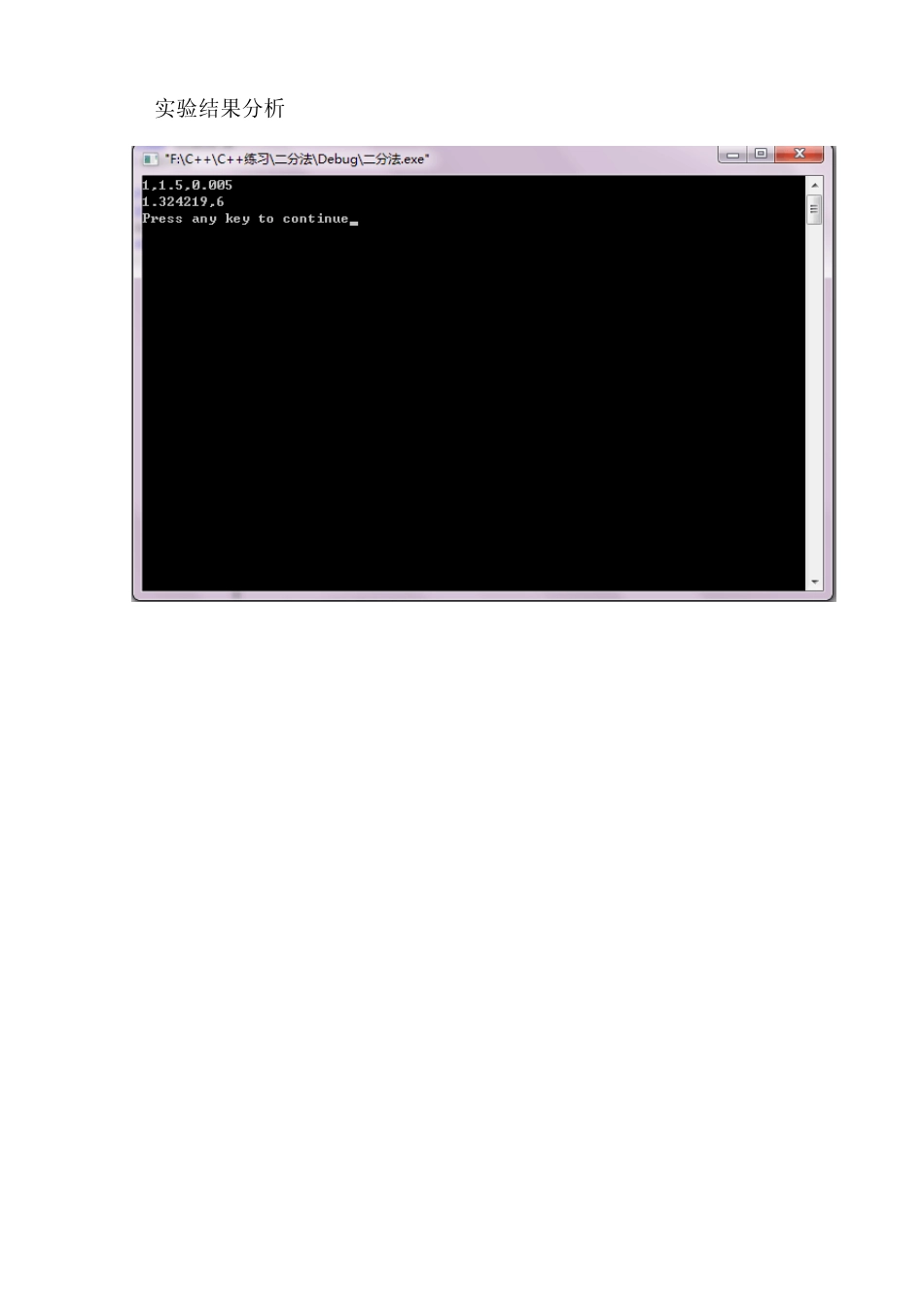
二分法 2 .2 算法步骤 步骤1: 准备 计算f(x )在有根区间[a,b]端点处的值f(a),f(b). 步骤2: 二分 计算f(x )在区间中点 (a+b)/2 处的值 f((a+b)/2). 步骤3: 判断 若f((a+b)/2)=0,则(a+b)/2 即是根,计算过程结束,否则检验; 若f((a+b)/2)f(a)<0,则以(a+b)/2 代替b,否则以(a+b)/2 代替a. 反复执行步骤2 和步骤3,直到区间[a,b]的长度小于允许误差e,此时中点(a+b)/2 即为所 求近似根。 2 .3 程序流程图 开始 a,b,e k =0 x 0=(a+b)/2 f (a)f(x 0)=c c<0 c=0 x 0=b 输出x 0,k x 0=b STOP b-a<=e 输出x 0,k STOP k +1=k N Y Y Y N 3 实验结果分析 #include"stdio.h" void main() { float a,b,e,x,c; int k=0,n=1; scanf("%f,%f,%f",&a,&b,&e); while(n==1) { x=(a+b)/2;c=(x*x*x-x-1)*(a*a*a-a-1); if(c<0) { b=x; if(b-a<=e) { printf("%f,%d\n",x,k); break;} else k++;} else { if(c==0) { printf("%f,%d\n",x,k); break;} else { a=x; if(b-a<=e) { printf("%f,%d\n",x,k); break;} else k++; }}}} 高斯塞德尔迭代法求方程组解 高斯主元素消去法求方程组解 2 .2 算法步骤 高斯塞德尔迭代法: 步骤1:给定初值)0(1)0(2)0(1,...,,nxxx ,精度 ,最大容许迭代次数M,令k=1。 步骤2:对 i=1,2,…,n 依此计算)0()1()0()1(01)0()1()1().(iiiiiiinjjjijiixxxxeaxaxx 步骤3:求出 e=}{max1inie,若 e< ,则输出 )0(ix(i=1,2,..,n ),停止计算。否则执行步 步骤4:若 k