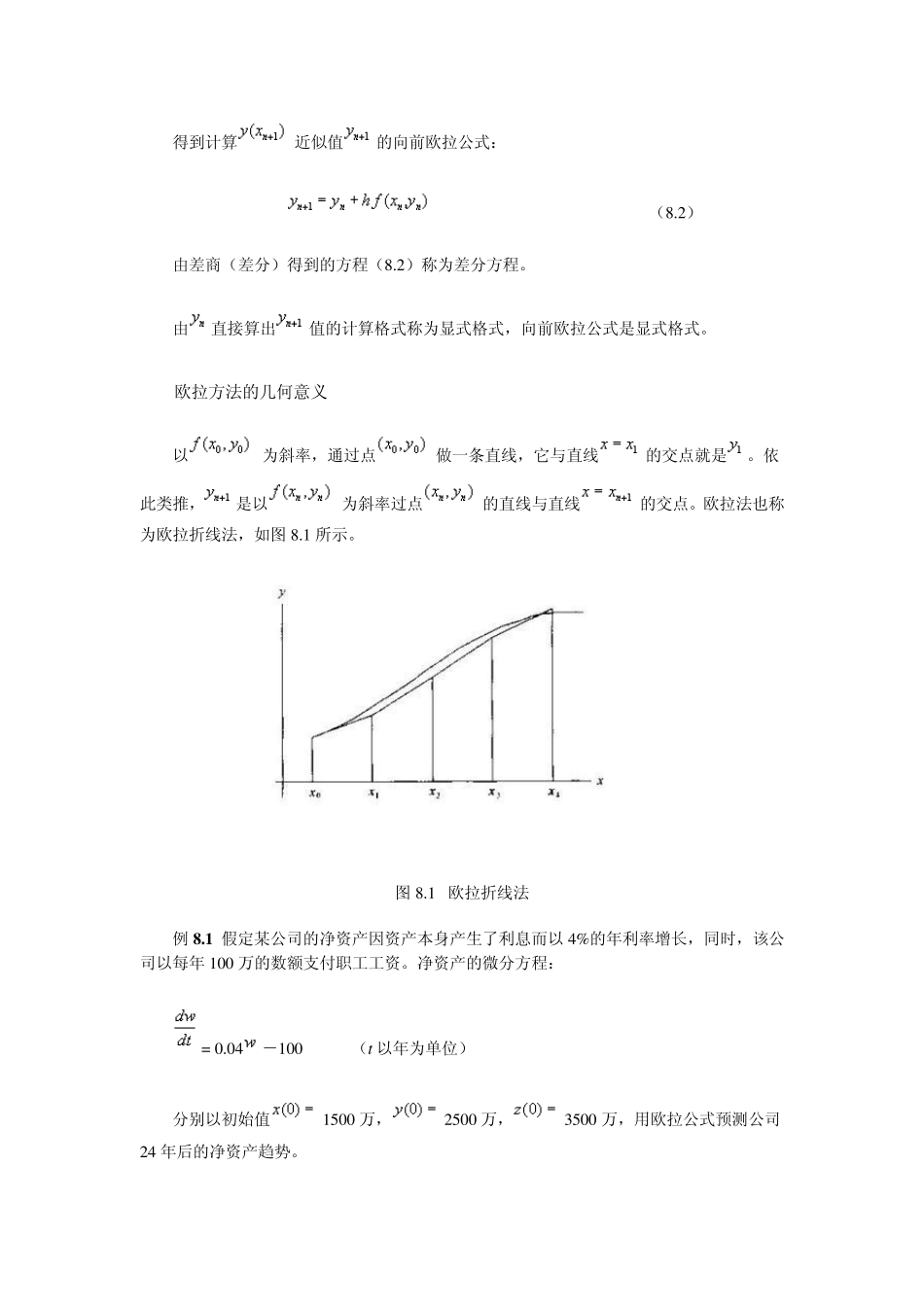
第8 章 常微分方程数值解 在描述系统的动态演变时,例如,物种的增长和蜕变,物体的运动,电路的振动瞬变,化学反应过程等,都能将其表示为以时间为变量的常微分方程或方程组。 物体冷却过程的数学模型可用下式表示: 它含有自变量、未知函数以及它的一阶导数,是一个常微分方程。在微分方程中我们称只有一个自变量函数的微分方程为常微分方程,自变量函数个数为两个或两个以上的微分方程为偏微分方程。给定微分方程及其初始条件,称为初值问题;给定微分方程及其边界条件,称为边值问题。 本章主要讨论常微分方程的初值问题: (8.1) 或记为 只有一些特殊形式的 ,才能找到它的解析解;对于大多数常微分方程的初值问题,主要用数值方法在计算机上求它的数值解。常微分方程初值问题的数值解是求在求解区间上剖分点列的数值解。在计算中约定表示常微分方程准确解的值,表示的近似值。本章介绍求解微分方程的差分数值方法。解常微分方程初值问题的主要手段是差分方法,这是一种通用性强适用面广的简单方法。 通常我们假定(8.1)中满足李普希兹(Lipschitz )条件,即存在常数,使对,有 则初值问题(8.1)的解存在且惟一。 8.1 欧拉(Euler)公式 8.1.1 基于差商的欧拉公式 对于常微分方程初值问题[式(8.1)],在求解区间上作等距分割的剖分,步长,记。用数值微商的方法,即用差商近似微商数值求解常微分方程。 用向前差商近似 做出的在处的一阶向前差商式: 又,于是得到 而的近似值可按 或 求得。类似地,由 以及 得到计算 近似值的向前欧拉公式: (8.2) 由差商(差分)得到的方程(8.2)称为差分方程。 由直接算出值的计算格式称为显式格式,向前欧拉公式是显式格式。 欧拉方法的几何意义 以为斜率,通过点做一条直线,它与直线的交点就是。依此类推,是以为斜率过点的直线与直线的交点。欧拉法也称为欧拉折线法,如图 8.1 所示。 图 8.1 欧拉折线法 例 8 .1 假定某公司的净资产因资产本身产生了利息而以 4%的年利率增长,同时,该公司以每年 100 万的数额支付职工工资。净资产的微分方程: = 0.04-100 (t 以年为单位) 分别以初始值 1500 万,2500 万,3500 万,用欧拉公式预测公司24 年后的净资产趋势。 解:。 分别以1 5 0 0 ,2 5 0 0 ,3 5 0 0 代入,计算结果见表 8 .1 。 表 8 .1 计算结果 1 2 3 4 9 1 0 1 1 1 2 1 3 1 4 1 5 1 6 ...