数值计算方法教案_曲线拟合与函数逼近

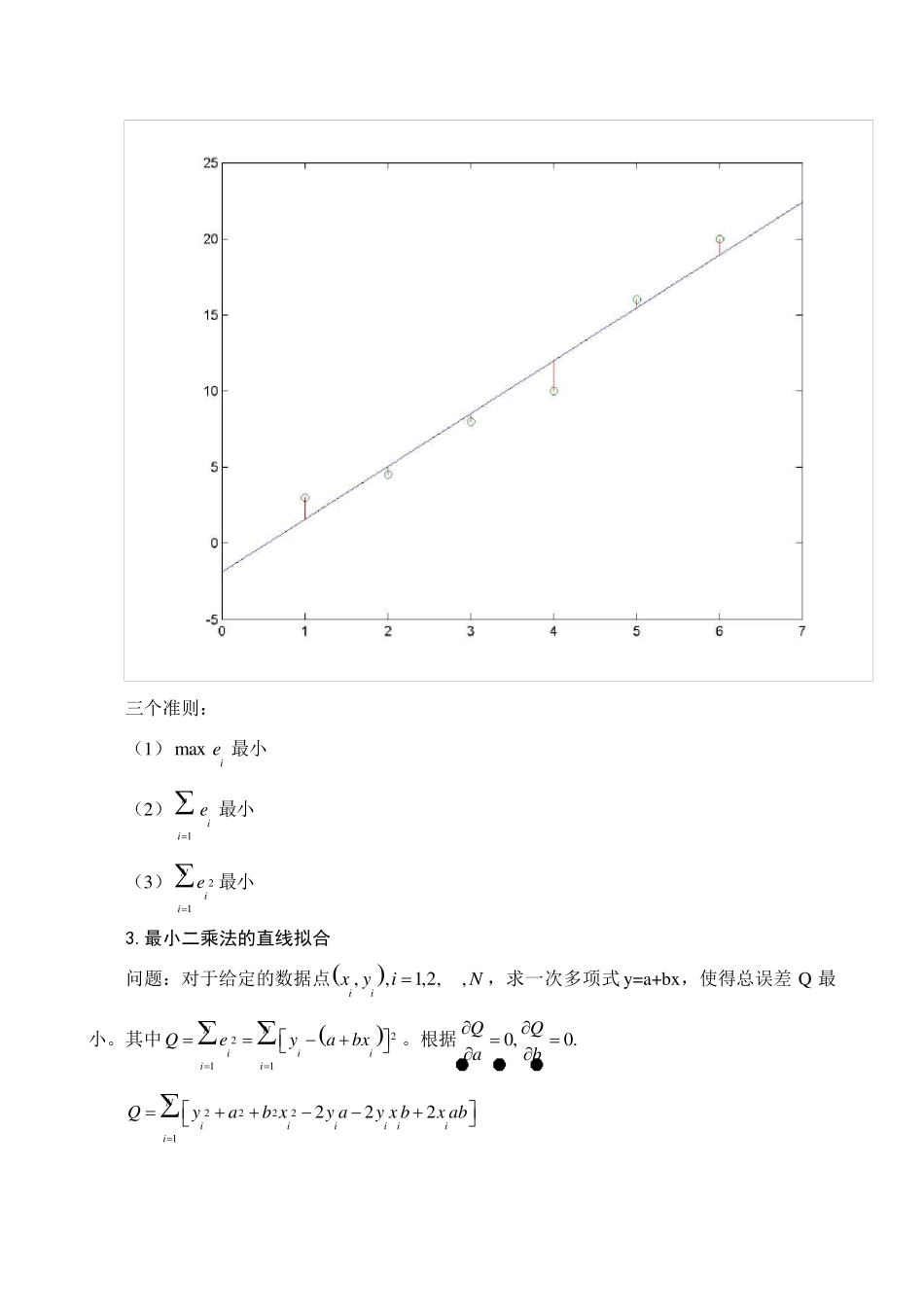
第三章 曲线拟合与函数逼近 一．曲线拟合 1.问题提出： 已知多组数据,,1,2,,iixyiN，由此预测函数 yf x的表达式。 数据特点：（1）点数较多。（2）所给数据存在误差。 解决方法：构造一条曲线反映所给数据点的变化总趋势，即所谓的“曲线拟合”。 2.直线拟合的概念 设直线方程为 y =a+bx 。 则残差为：ˆiiieyy,1,2,,iN，其中 ˆiiyabx。 残差ie 是衡量拟合好坏的重要标志。 可以用 MATLAB 软件绘制残差的概念。 x =1:6; y =[3,4.5,8,10,16,20]; p=poly fit(x ,y ,1); x i=0:0.01:7; y i=poly v al(p,x i); plot(x i,y i,x ,y , 'o'); y 1=poly v al(p,x ); hold on for i=1:6 plot([i,i],[y (i),y 1(i)], 'r'); end 可以绘制出如下图形： 三个准则： （1）maxie 最小 （2）1niie最小 （3）21Niie最小 3.最小二乘法的直线拟合 问题：对于给定的数据点,,1,2,,iix yiN，求一次多项式y=a+bx，使得总误差Q 最小。其中 2211NNiiiiiQeyabx。根据0,0.QQab 22221222NiiiiiiiQyab xy ay xbx ab 12222NiiiiiQayx bNaybxa 2212222NiiiiiiiiiQbxy xx abxx yaxb 故有以下方程组（正则方程）： 2iiiiiiaNbxyaxbxx y 例1.给定数据表，求最小二乘拟合一次多项式 x i 165 123 150 123 141 y i 187 126 172 125 148 解：N=5，51iix=702，51iiy=758，521iix=99864，51iiix y=108396。 则有方程组 570275870299864108396abbb 解得 a=-60.9392，b=1.5138，则一次多项式为 y =-60.9392+1.5138b 用 MATLAB 计算并画图如下： x =[165,123,150,123,141]; y =[187,126,172,125,148]; A(1,1)=5;A(1,2)=su m(x );A(1,3)=su m(y ); A(2,1)=su m(x );A(2,2)=su m(x .^2);A(2,3)=x *y '; B=rref(A); a=B(1,3);b=B(2,3); p=[b,a]; %以上四行，可以用一行命令 p=poly fit(x ,y ,1); 替代。 x i=min(x )-1:0.01:max (x )+1; y i=poly v al(p,x i); plot(x i,y i,x ,y , 'o'); 绘制如下图形 4.最小二乘法的多项式拟合 问题：对于给定的数据点,,1,2,,iix y iN，求m 次多...