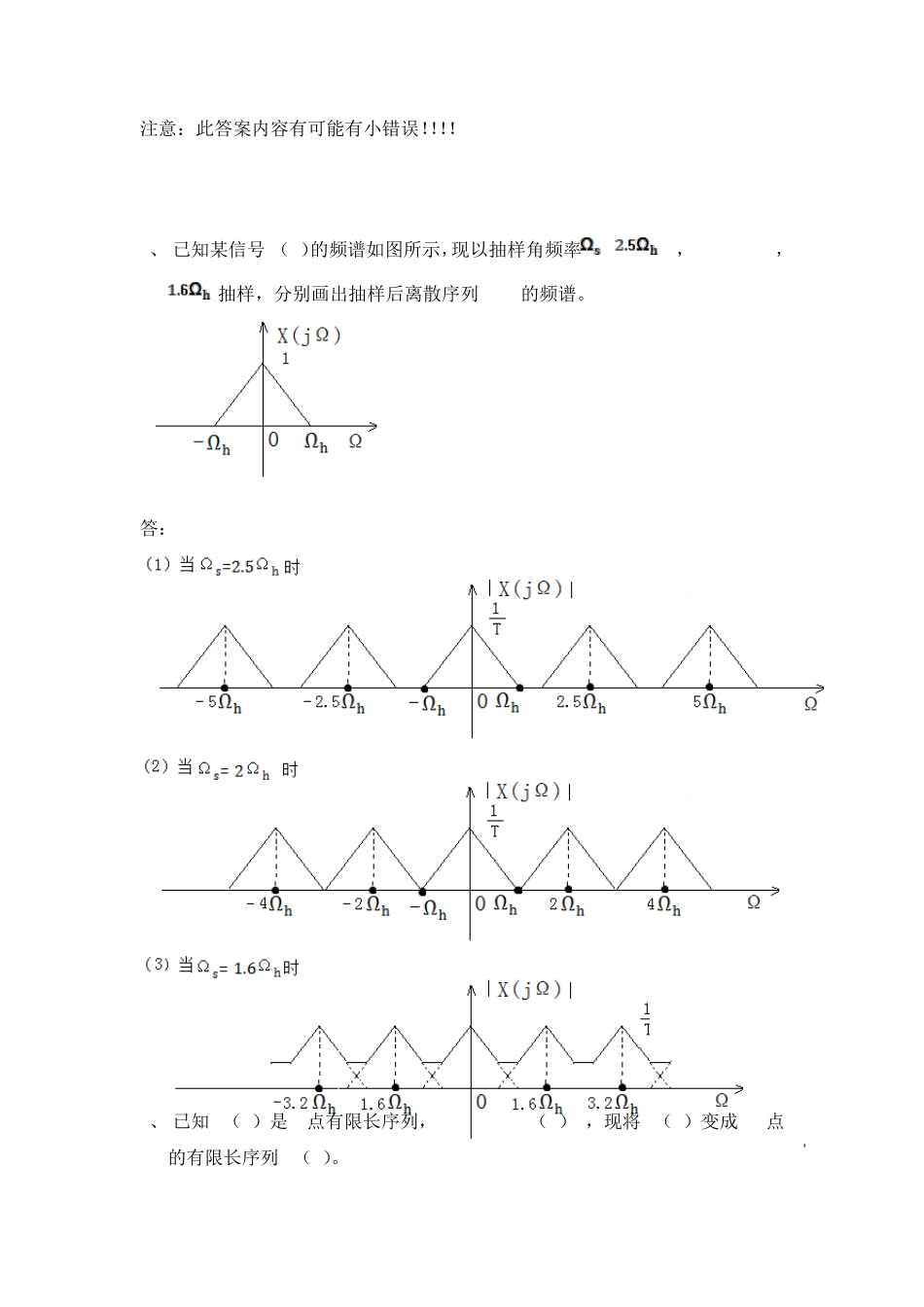
注意:此答案内容有可能有小错误!!!! 1、 已知某信号 x(t)的频谱如图所示,现以抽样角频率= , ,抽样,分别画出抽样后离散序列 x[n]的频谱。 答: 2、 已知 x(n)是 N点有限长序列,X(K)=DFT[x(n)],现将 x(n)变成 rN点的有限长序列 y(n)。 试求DFT[y(n)](rN点DFT)与X(K)的关系。 答:,0-1 = ==X(),k=lr(l=0,1,……N-1) 在一个周期内,Y(k)的抽样点数是 X(k)的r倍,相当于在 X(k)的每两个值之间插入(r-1)的其他的数值(不一定为零),而当 k为 r的整数 l倍时,Y(k)与X()相等。 3、 设序列的长度 M=8,其值是:,现分别对的离散时间傅里叶变换在一个周期内作 N=6点均匀抽样,得,试分析(K)的反变换和原序列的关系。 答:知识点:频域抽样,时域周期延拓 即频域抽样,时域周期延拓。 4、 试叙述利用 DFT做连续信号的谱分析时的一般过程及在此过程中产生的问题和参数选取的原则。 答:一般过程 :,(抽样、截短、周期延拓、取一个周期,谱分析) 产生的问题和参数选取的原则: (1)频谱混叠失真抽样频率,频率分辨力,其中为时域记录长度; (2)频谱泄露较小频谱泄露的方法:窗宽加宽;不要突然截断; (3)栅栏效应:增加频域抽样点数(在不改变时域的前提下,可以添加零值点)。 5、 试利用圆周卷积和线性卷积的关系以及时域圆周卷积定理说明利用 DFT求解两序列线性卷积的方法。 答:大前提:设序列的长度为, 的长度为, ; (1)圆周卷积和线性卷积的关系: (2)时域圆周卷积定理:时域卷积,频域相乘。 N点DFT记作, N点DFT记作, 6、 频谱分析的模拟信号以10KHZ被抽样,计算了 1024点DFT,试确定频谱抽样之间的频率间隔,并回答其中 1024点DFT中的X(0),X(512)所对应的频率。 知识点:信号记录长度,抽样间隔 T,频率分辨力=频谱抽样频率间隔,信号最高频率,抽样频率 答: ,所以频谱抽样之间的频率间隔 , X(0),X(512)所对应的频率分别为 7、 已知序列 ,试求 x(n)的6点离散傅里叶变换 、12点离散傅里叶变换和 x(n)的离散时间傅里叶变换,并说明和的关系,并作图表示。 答:(1) (2) (3) (4)和的关系: 如下图所示: 8、 已知是一个长度为 16的有限长序列,求它的 16点 DFT,是一个长度为 12的有限长序列,求它的 12点 DFT。 注:离散时间傅里叶变换,离散傅里叶变换 X(k) 答:(1),其中 综上所述 (2),其中 ...