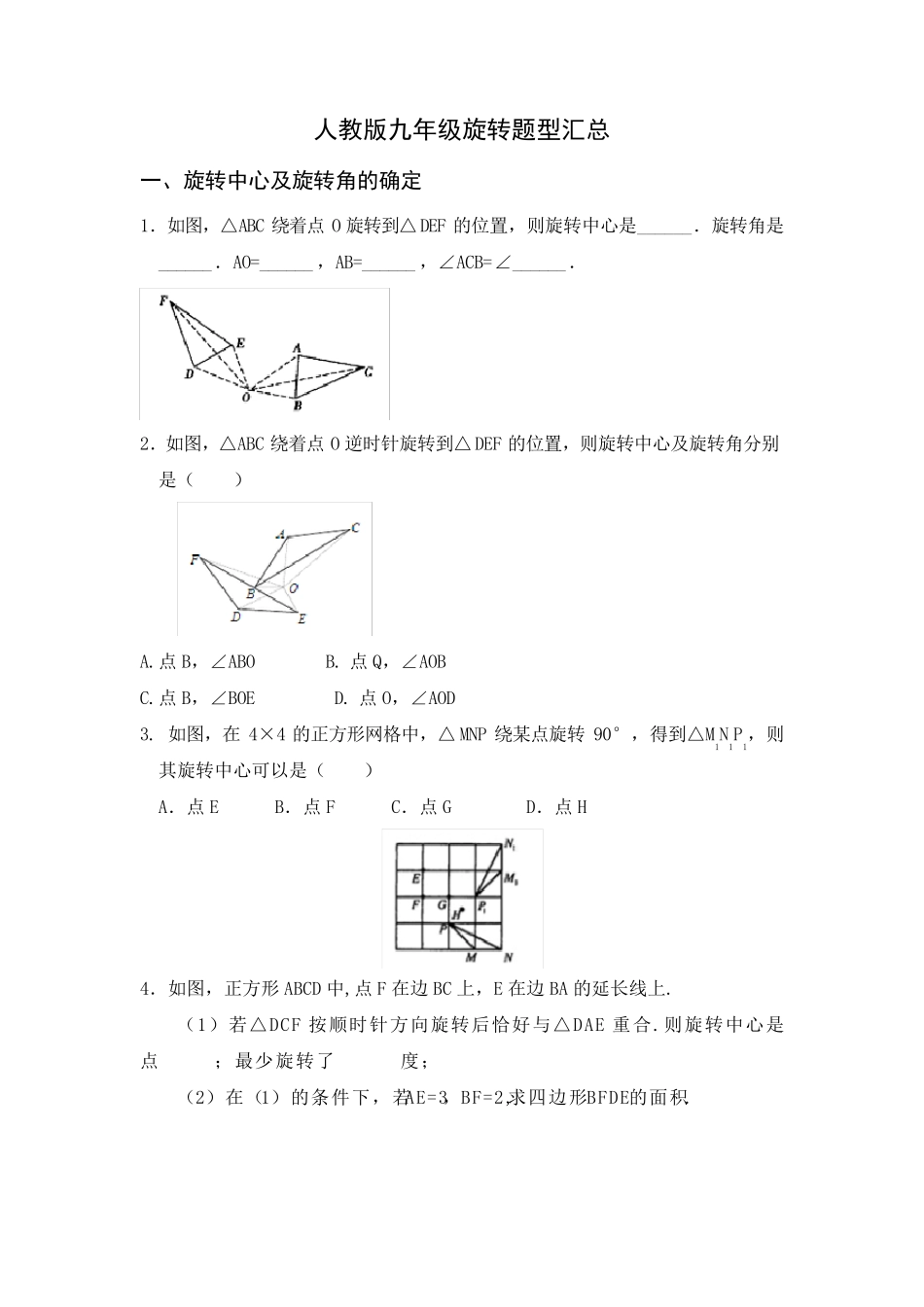
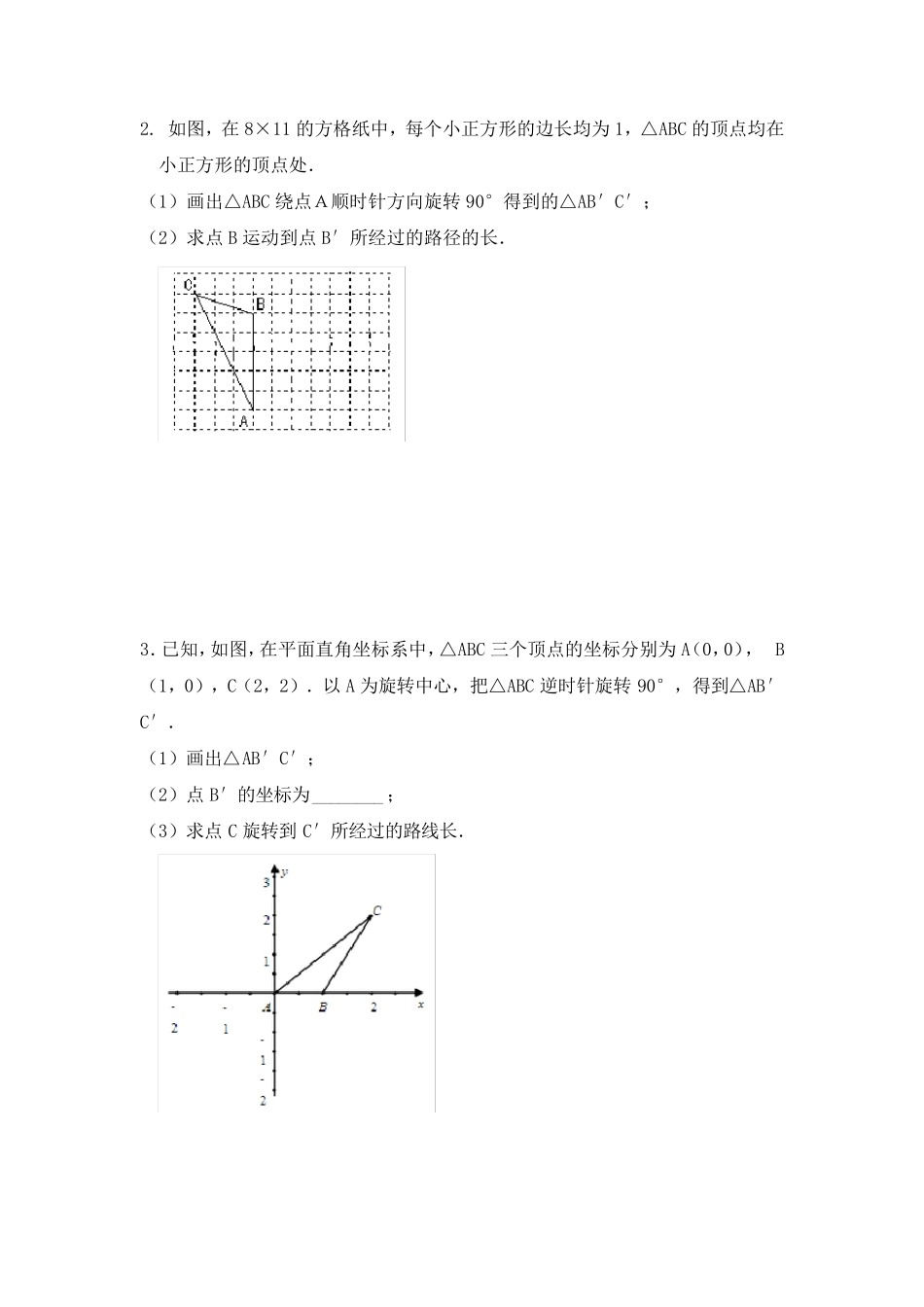
人教版九年级旋转题型汇总 一、旋转中心及旋转角的确定 1.如图,△ABC 绕着点O 旋转到△DEF 的位置,则旋转中心是______.旋转角是______.AO=______ ,AB=______ ,∠ACB=∠______. 2.如图,△ABC 绕着点O 逆时针旋转到△DEF 的位置,则旋转中心及旋转角分别是( ) A.点B,∠ABO B. 点Q,∠AOB C.点B,∠BOE D. 点O,∠AOD 3. 如图,在4×4 的正方形网格中,△MNP 绕某点旋转90°,得到△M1N1P1,则其旋转中心可以是( ) A.点E B.点F C.点G D.点H 4.如图,正方形ABCD 中,点F 在边 BC 上,E 在边 BA 的延长线上. (1)若△DCF 按顺时针方向旋转后恰好与△DAE 重合.则旋转中心是点 ;最少旋转了 度; (2)在(1)的条件下,若AE=3,BF=2,求四边形BFDE的面积. 二、旋转图形的做法 1. 在平面直角坐标系中,等腰Rt△OAB 斜边OB 在y 轴上,且OB=4. (1)画出△OAB 绕原点O 顺时针旋转90°后得到的三角形△OA′B′; (2)求点A 在旋转过程中经过的路径长. 2. 如图,在8×11 的方格纸中,每个小正方形的边长均为1,△ABC 的顶点均在小正方形的顶点处. (1)画出△ABC 绕点A顺时针方向旋转90°得到的△AB′C′; (2)求点B 运动到点B′所经过的路径的长. 3.已知,如图,在平面直角坐标系中,△ABC 三个顶点的坐标分别为A(0,0), B(1,0),C(2,2).以 A 为旋转中心,把△ABC 逆时针旋转90°,得到△AB′C′. (1)画出△AB′C′; (2)点B′的坐标为________ ; (3)求点C 旋转到 C′所经过的路线长. 4. 如图,Rt△ABC 中,∠C=90°,∠A=30°,AB=2. (1)用尺规作图,作出△ABC 绕点 A 逆时针旋转 60°后得到的△AB1C1(不写画 法,保留画图痕迹); 结论:__________________为所求。 (2)在(1)的条件下,连接 B1C,求 B1C 的长。 5.如图,在 8×8 正方形网格中,每个小正方形的边长均为 1 个单位长度.将格点△ABC 向下平移 4 个单位长度,得到△A’B’C’,再把△A’B’C’绕点 O 顺时针旋转 90°,得到△A”B”C”,请你画出△A’B’C’和△A”B”C”. 6.在平面直角坐标系 xOy 中,已知△ABC 三个顶点的坐标分别为 A(-1,2),B(-3,4),C(-2,9). (1)画出△ABC; (2)画出△ABC 绕点 A 顺时针旋转 90°后得到的△AB1C1,并求出 CC1的长. 三、对称中心的找法 1.已知:如图,四边形ABCD 与四边形...