两端铰支一端固定VIP免费

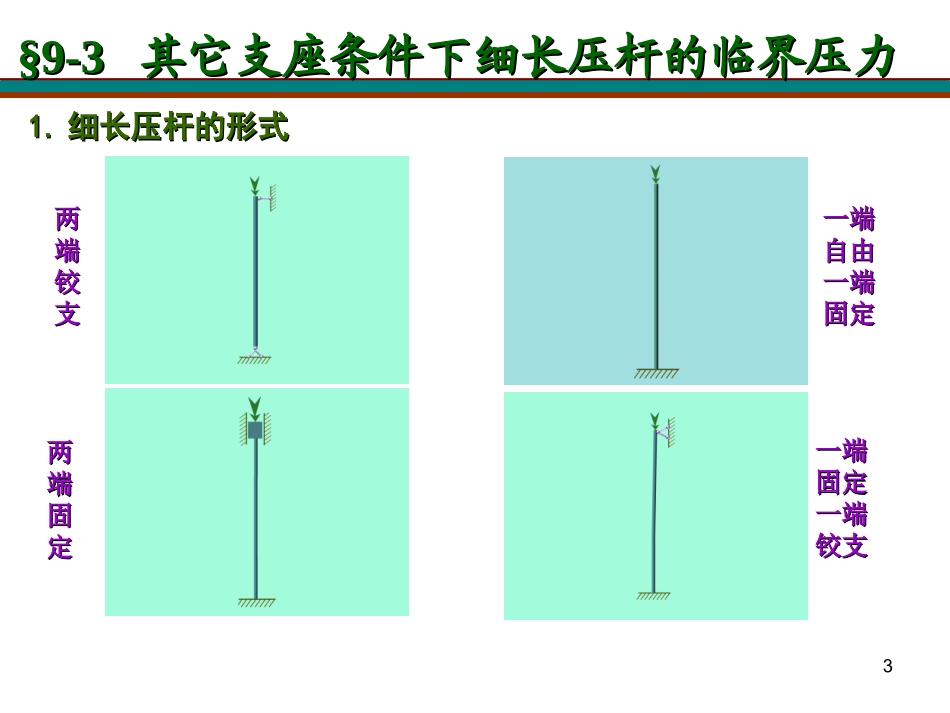
1第九章压杆稳定§9-3§9-3其它支座条件下细长压杆的临界压力其它支座条件下细长压杆的临界压力23§9-3§9-3其它支座条件下细长压杆的临界压力其它支座条件下细长压杆的临界压力1.1.细长压杆的形式细长压杆的形式两两端端铰铰支支一端一端自由自由一端一端固定固定一端一端固定固定一端一端铰支铰支两两端端固固定定2.2.其它支座条件下的欧拉公式其它支座条件下的欧拉公式lFcr2l()2cr22EIFlFcrl0.3l0.7l(.)2cr207EIFlFcrl2cr2EIFllFcrl/4l/4l/2(/)2cr22EIFll§9-3§9-3其它支座条件下细长压杆的临界压力其它支座条件下细长压杆的临界压力45两端铰支两端铰支一端固定，另一端铰支一端固定，另一端铰支两端固定两端固定一端固定，另一端自由一端固定，另一端自由表表9-19-1各种支承约束条件下等截面细长压杆各种支承约束条件下等截面细长压杆临界力的欧拉公式临界力的欧拉公式支承情况支承情况临界力的欧拉公式临界力的欧拉公式长度因数长度因数=1=1=0.7=0.7=0.5=0.5=2=2欧拉公式的统一形式欧拉公式的统一形式（（为压杆的长度因为压杆的长度因数）数）22crπlEIF22cr)7.0(πlEIF22cr)5.0(πlEIF22cr)2(πlEIF22cr)(πlEIF§9-3§9-3其它支座条件下细长压杆的临界压力其它支座条件下细长压杆的临界压力65.5.讨论讨论为长度因数为长度因数ll为相当长度为相当长度（（11）相当长度）相当长度ll的物理意义的物理意义压杆失稳时，挠曲线上两拐点间的长度就是压杆的相压杆失稳时，挠曲线上两拐点间的长度就是压杆的相当长度当长度ll..ll是各种支承条件下，细长压杆失稳时，挠曲线中相当于是各种支承条件下，细长压杆失稳时，挠曲线中相当于半波正弦曲线的一段长度半波正弦曲线的一段长度..22cr)(πlEIF§9-3§9-3其它支座条件下细长压杆的临界压力其它支座条件下细长压杆的临界压力7zyx取取IIyy，，IIzz中小的一个计算临界力中小的一个计算临界力..若杆端在各个方向的约束情况不同（如柱若杆端在各个方向的约束情况不同（如柱形铰），应分别计算杆在不同方向失稳时的临形铰），应分别计算杆在不同方向失稳时的临界压力界压力..II为其相应中性轴的惯性矩为其相应中性轴的惯性矩..即分别用即分别用IIyy，，IIzz计算出两个临界计算出两个临界压力压力..然后取小的一个作为压杆的临界压力然后取小的一个作为压杆的临界压力..（（22）横截面对某一形心主惯性轴的惯性矩）横截面对某一形心主惯性轴的惯性矩II若杆端在各个方向的约束情况相同（如球形铰等），若杆端在各个方向的约束情况相同（如球形铰等），则则II应取最小的形心主惯性矩应取最小的形心主惯性矩..§9-3§9-3其它支座条件下细长压杆的临界压力其它支座条件下细长压杆的临界压力8例题例题11已知一已知一内燃机、空气压缩机的内燃机、空气压缩机的连杆为细长压杆连杆为细长压杆..截面形截面形状为工字钢形，惯性矩状为工字钢形，惯性矩IIzz=6.5×10=6.5×1044mmmm44,,IIyy=3.8×10=3.8×1044mmmm44，弹性模，弹性模量量EE=2.1×10=2.1×1055MPaMPa..试计算临界力试计算临界力FFcrcr..x8801000yzyxz880§9-3§9-3其它支座条件下细长压杆的临界压力其它支座条件下细长压杆的临界压力9FFlxz880（（11）杆件在两个方向的约束情况不同；）杆件在两个方向的约束情况不同；x8801000yzy（（22））计算出两个临界压力计算出两个临界压力..最后取小的一个作为压杆最后取小的一个作为压杆的临界压力的临界压力..分析思路：分析思路：§9-3§9-3其它支座条件下细长压杆的临界压力其它支座条件下细长压杆的临界压力10解：解：kN6.134)11(105.6101.214.3)(π2811222crlEIFx8801000yzykN4.406)88.05.0(108.3101.214.3)(π2811222crlEIF所以连杆的临界压力为所以连杆的临界压力为134.6kN.134.6kN.xOyxOy面：约束情况为两端铰支面：约束情况为两端铰支=1=1，，II==IIzz，，ll=1m=1mxOzxOz面：约束情况为两端固定面：约束情况为两端固定=0.5=0.5，，II==IIyy，，ll=0.88m=0.88mFFlxz880§9-3§9-3其它支座条件下细长压...