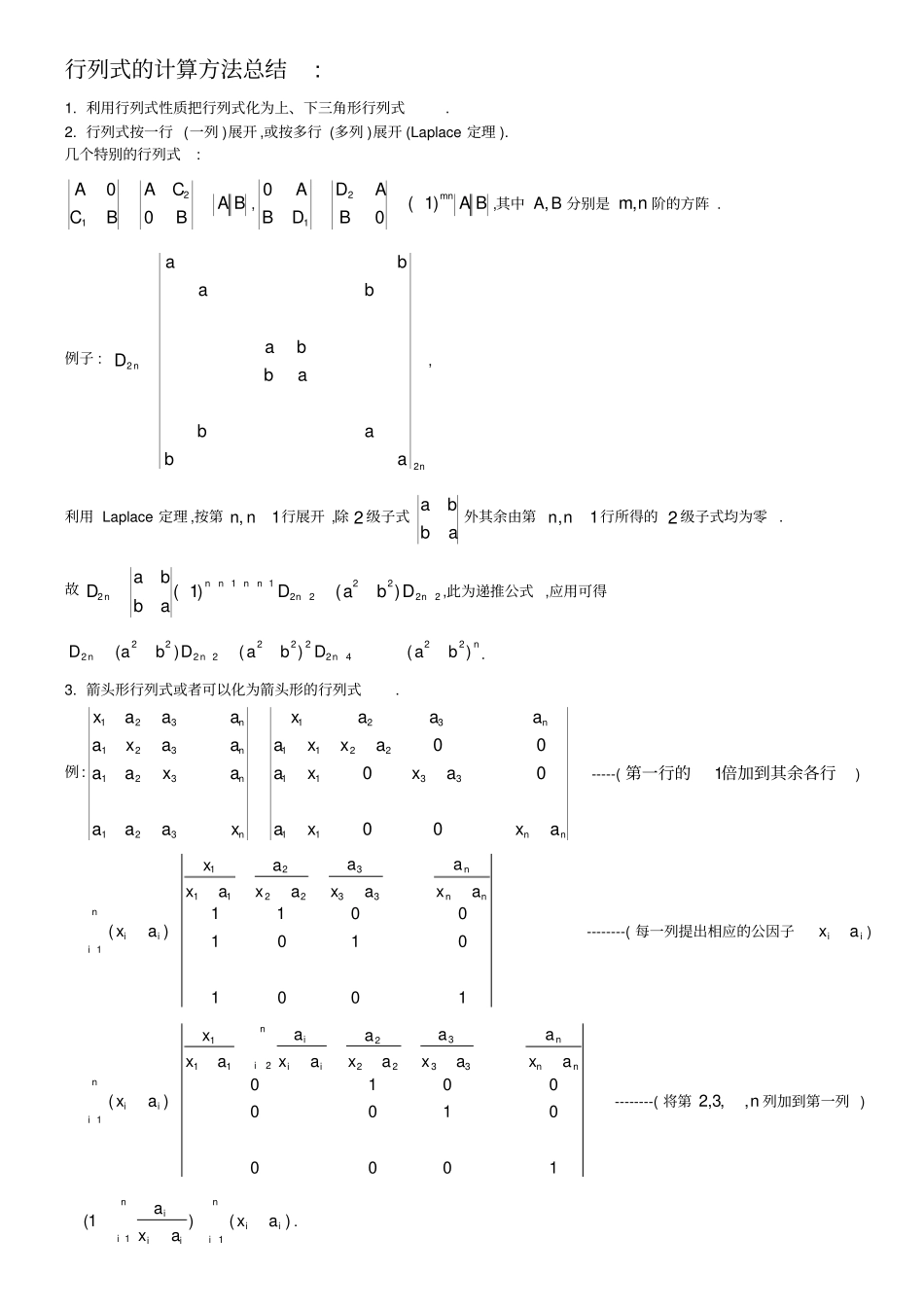
行列式的计算方法总结: 1. 利用行列式性质把行列式化为上、下三角形行列式. 2. 行列式按一行 (一列 )展开 ,或按多行 (多列 )展开 (Laplace 定理 ). 几个特别的行列式: BABCABCA0021,BABADDBAmn)1(0021,其中BA,分别是nm,阶的方阵 . 例子 : nnabababbababaD22, 利用 Laplace 定理 ,按第1, nn行展开 ,除 2 级子式abba外其余由第1,nn行所得的 2 级子式均为零 . 故222222112)()1(nnnnnnnDbaDabbaD,此为递推公式 ,应用可得nnnnbaDbaDbaD)()()(224222222222. 3. 箭头形行列式或者可以化为箭头形的行列式. 例:nnnnnnnaxxaaxxaaxxaaaaxxaaaaxaaaaxaaaax0000001133112211321321321321321-----(倍加到其余各行第一行的1) 100101010011)(3332221111nnnniiiaxaaxaaxaaxxax--------( 每一列提出相应的公因子iiax) 100001000010)(33322221111nnnniiiiniiiaxaaxaaxaaxaaxxax--------( 将第n,,3,2列加到第一列 ) niiiniiiiaxaxa11)()1(. 其它的例子:特点是除了主对角线,其余位置上的元素各行或各列都相同. nxaaaaaxaaaaaxaaaaaxa321,nnnnaxaaaaaxaaaaaxaaaaax321321321321. 4. 逐行逐列相减法.行列式特点是每相邻两行(列)之间有许多元素相同.用逐行 (列)相减可以化出零. 5. 升阶法 (或加边法 , 添加一行一列 ,利于计算 ,但同时保持行列式不变). 例子 :nnnnnnnnnnnnnnbababaabababaabababaabbbbababababababababa10101010000011112122212212111121212221212111niiniiiniinniiniiiniinnbbanabbbbbanaaaabbb11121111212111100000100000100111111001010100111011101njnjiijijniiniiniiiniiniiaabbabanba1111111)(1)1)(1(. 例子 :nnxaaaaaxaaaaaxaaaaaxaaaaaxaaaaaxaaaaaxaaaaaxa00001321321).1(00000000000000001000100010001000111213211321niinnniinxaxxxxxxxaaaaxaxxxxaaaa6. 利用范德蒙德行列式. 计算行列式 : nnnnnnnnnnnnxxxxxxxxxxxxxxxxD321223222122322213211111解: 令: nnnnnnnnnnnnnnnnnyxxxyxxxyxxxyxxxyxxxD211112112222212222212111111,这是一个1n级范德蒙德行列式. 一方面 ,由范德蒙德行列式得)())(()(2111nnijjixyxyxyxxD.可看做是关于y 的一个 n 次多项式 . 另一方面 ,将1D 按最后一列展开,可得一个关于y 的多项式01111pypypypDnnnn,其中1ny的系数1np与所求行列式D 的关系为1npD. 由)())(()(2111nnijjixyxyxyxxD来计算1ny的系数1np得:niinijjinxxxp111)(, 故有niinijjinx...