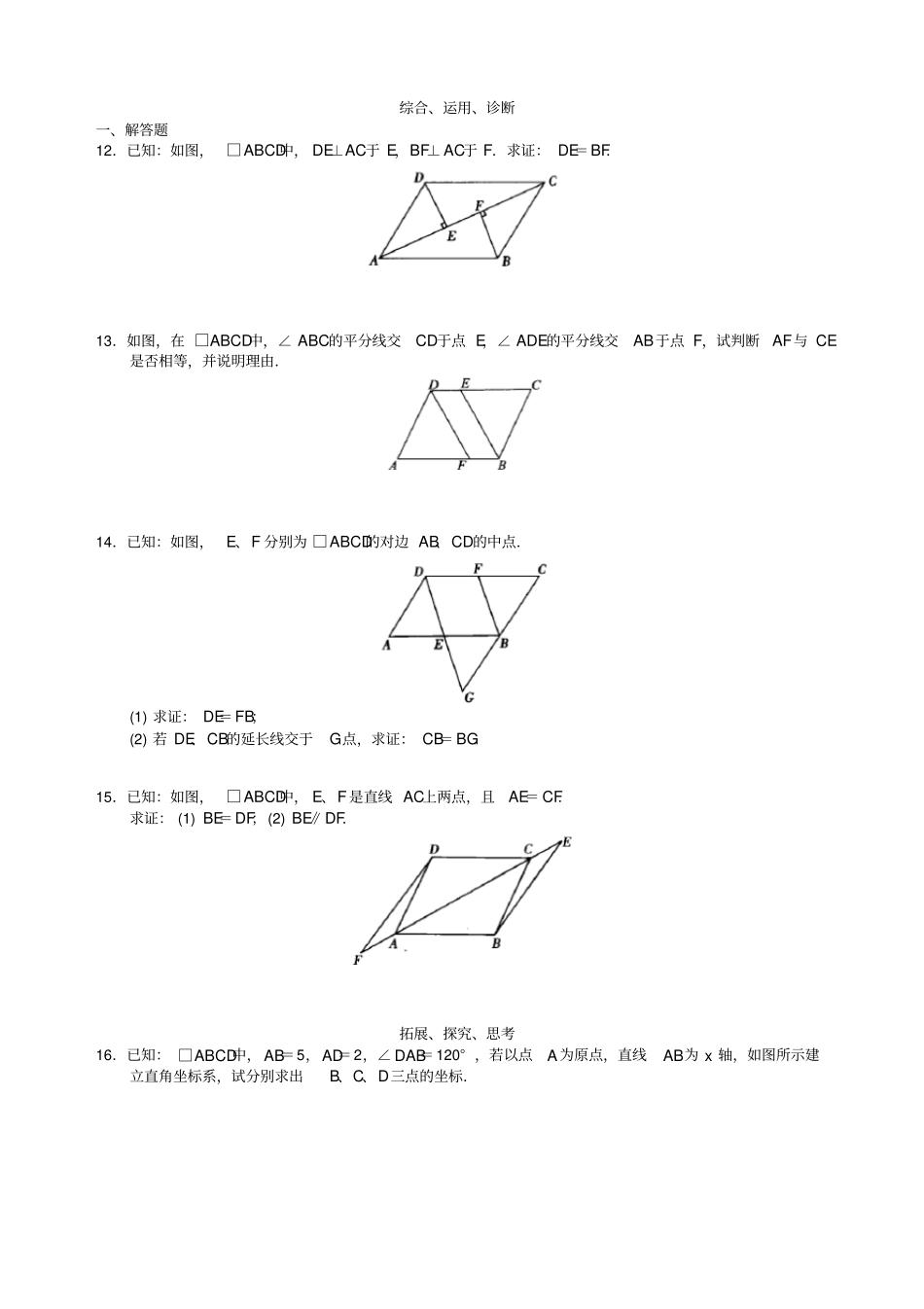
第十九章四边形测试 1 平行四边形的性质 ( 一)学习要求1.理解平行四边形的概念,掌握平行四边形的性质定理;2.能初步运用平行四边形的性质进行推理和计算,并体会如何利用所学的三角形的知识解决四边形的问题.课堂学习检测一、填空题1.两组对边分别______的四边形叫做平行四边形.它用符号“□”表示,平行四边形ABCD记作__________。2.平行四边形的两组对边分别______且 ______;平行四边形的两组对角分别______;两邻角 ______;平行四边形的对角线______;平行四边形的面积=底边长×______.3.在 □ABCD中,若∠ A-∠ B=40° ,则∠ A=______,∠ B=______.4.若平行四边形周长为54cm,两邻边之差为5cm,则这两边的长度分别为______.5.若 □ABCD的对角线 AC平分∠ DAB,则对角线AC与 BD的位置关系是 ______.6.如图, □ABCD中, CE⊥AB,垂足为 E,如果∠ A=115° ,则∠ BCE=______.6 题图7.如图,在 □ABCD中, DB=DC、∠ A=65° , CE⊥BD于 E,则∠ BCE= ______.7 题图8.若在 □ABCD中,∠ A=30° , AB=7cm,AD=6cm,则 S□ABCD=______.二、选择题9.如图,将 □ABCD沿 AE翻折,使点B 恰好落在 AD上的点 F 处,则下列结论不一定成立的是( ).(A) AF=EF(B) AB=EF(C) AE=AF(D) AF=BE10.如图,下列推理不正确的是( ).(A) AB∥CD ∴∠ ABC+∠ C=180°(B) ∠ 1=∠ 2 ∴AD∥ BC(C) AD∥BC ∴∠ 3=∠ 4(D) ∠ A+∠ ADC=180°∴ AB∥CD11.平行四边形两邻边分别为24 和 16,若两长边间的距离为8,则两短边间的距离为( ).(A)5 (B)6(C)8 (D)12综合、运用、诊断一、解答题12.已知:如图,□ABCD中, DE⊥AC于 E,BF⊥ AC于 F.求证: DE=BF.13.如图,在 □ABCD中,∠ ABC的平分线交CD于点 E,∠ ADE的平分线交AB于点 F,试判断AF与 CE是否相等,并说明理由.14.已知:如图,E、F 分别为 □ABCD的对边 AB、CD的中点.(1) 求证: DE=FB;(2) 若 DE、CB的延长线交于G点,求证: CB= BG.15.已知:如图,□ABCD中, E、F是直线 AC上两点,且AE= CF.求证: (1) BE=DF;(2) BE∥DF.拓展、探究、思考16.已知: □ABCD中, AB=5,AD=2,∠ DAB=120° ,若以点A 为原点,直线AB为 x 轴,如图所示建立直角坐标系,试分别求出B、C、D三点的坐标.17.某市要在一块□ABCD的空地上...