有效非线性光学系数

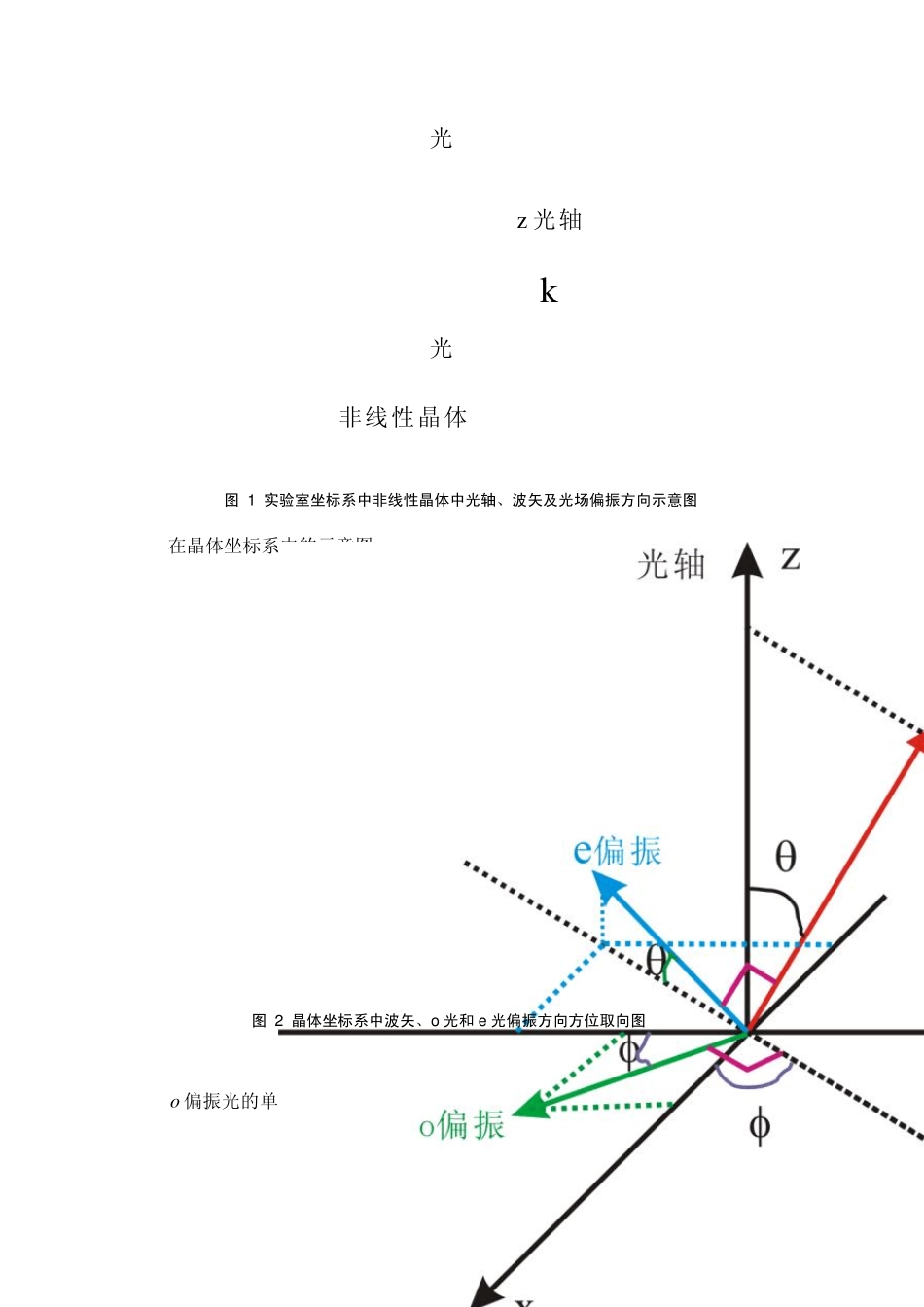
1 §2 .4 有效非线性光学系数 由上节的讨论可以看到，为了高效率率地产生二次谐波，除了采用具有高非线性介质外，还应满足相位匹配条件。在实际工作中，人们引入了有效非线性系数effd的概念，并指出，为了有效地产生二次谐波，希望effd愈大愈好。 2 .4 .1 有效非线性极化率 在求解三波混频的耦合波方程时，引入了有效非线性极化率 2eff。例如         223312122312312;,;,effaaaaaa     (2.4.1-1) 有效非线性极化率除表征介质的非线性特性外，还与混频光场的偏振方向有关。 有效非线性极化率实际上表示了频率为1 和2 的两个单位光电场，通过二阶极化率张量 2312;,  产生频率为3 的非线性极化强度在  3a 方向上的投影。耦合波方程的解与有效非线性极化率有关，而不与非线性极化率张量中每个元素单独发生关系。从物理上来看这是很显然的，因为所产生的非线性极化强度中只有与  3a 方向一致的分量才与  3a 偏振方向的入射光波发生耦合，而与  3a 偏振方向垂直的分量与  3a 偏振方向的入射光波不发生耦合。 用耦合波方程解释 ：     323333i kzEziaPz ezn c (2.4.1-2) 2 .4 .2 几种非线性匹配方式： 为在晶体中达到相位匹配，参与非线性相互作用的三个光波应取特定的偏振方向。 表1 两类匹配四种相互作用方式 I 类匹配 II 类匹配 正单轴晶体 eeo  eoo 负单轴晶体 ooe oee  2 在晶体坐标系中的示意图： o 偏振光的单位矢量矩阵为：sincos0oa ， e 偏振光的单位矢量矩阵为：kz 光轴o光e光非线性晶体 图 1 实验室坐标系中非线性晶体中光轴、波矢及光场偏振方向示意图 图 2 晶体坐标系中波矢、o 光和 e 光偏振方向方位取向图 3 cos coscos sinsinea 2 .4 .3 有效非线性光学系数计算 在非线性光学中，除了采用非线性极化率张量 2描述非线性作用外，习惯上，特别对实验工作者采用非线性光学系数d描述非线性相互作用。 d与 2有如下关系。   21212,,d  ...