有限元4薄板弯曲问题

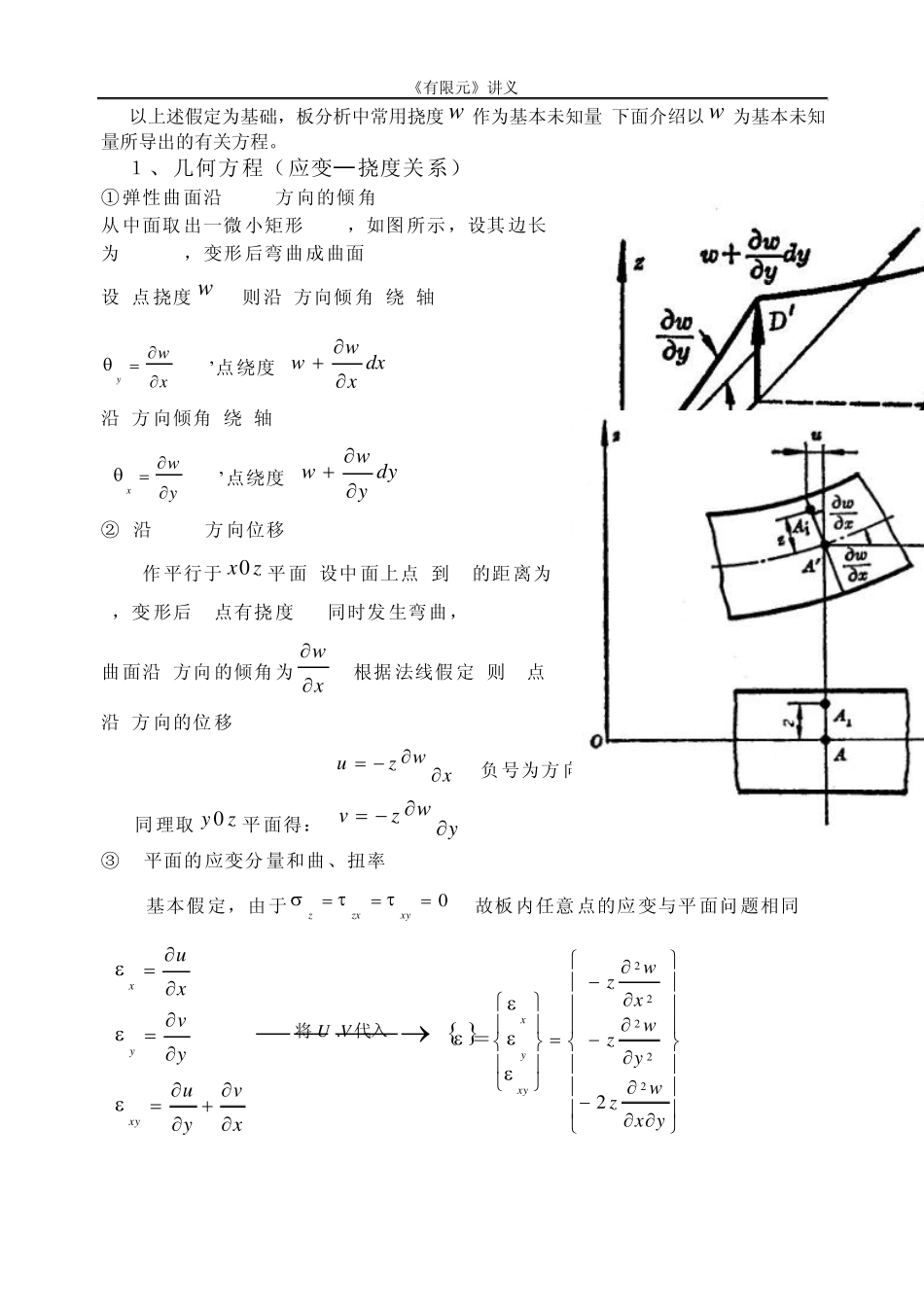
《有限元》讲义 1 第4章 弹性薄板弯曲问题的有限元法 薄板弯曲问题在理论上和应用上都具有重要意义,并有专门著作加以论述（如杨耀乾《平板理论》）。象其它弹性力学问题一样，用微分方程、差分法等经典方法所能求解的薄板问题很有限，一般只能解决等厚、小孔口、支承情况较简单的单跨板。故工程设计中以往多采用简化、近似、图表等方法来解决板的设计问题。 在板的分析中，常取板的中面为xoy平面(如图)。平板结构按其厚度t与短边a的比值大小而分为: 厚板（Thick plate）和 薄板（Thin plate)两种。 当1at时称为薄板 平板上所承受的荷载通常有两种: 1. 面内拉压荷载。 由面内拉压刚度承担, 属平面应力问题。 2. 垂直于板的法向荷载, 弯扭变形为主,具有梁的受力特征, 即常说的弯曲问题。平板在垂直于板面的荷载作用下产生挠度W。 当最大挠度w远小于t时, 称为小挠度问题(or刚性板)(stiffness plate) 当最大挠度w与t相差不大时,称为大挠度问题(or柔性板)(flexure plate) (工程定义: 51tw 为刚性板；551tw为柔性板； 5tw 为绝对柔性板。) 4.1 基本理论 一、基本假定 １、略去垂直于中面的法向应力。（0z），即以中面上沿Z方向的挠度W代表板的挠度) ２、变形前垂直中面的任意直线，变形后仍保持为垂直中面的直线。（─法向假定0zx,0zy） ３、板弯曲时，中面不产生应力。(─中面中性层假定) 上述假定常称为薄板小挠度问题假定（or 柯克霍夫假定）。符合上述假定的平板即为刚性板。 二、基本方法 《有限元》讲义 2 以上述假定为基础，板分析中常用挠度w 作为基本未知量,下面介绍以w 为基本未知量所导出的有关方程。 １、几何方程（应变─挠度关系） ①弹性曲面沿x, y 方向的倾角 从中面取出一微小矩形ABCD，如图所示，设其边长为dx, dy，变形后弯曲成曲面A'B'C'D' 设A点挠度w , 则沿x方向倾角(绕y轴) xwy (B’点绕度 dxxww) 沿y方向倾角(绕x轴) ywx (D’点绕度 dyyww) ② 沿x, y 方向位移 作平行于zx0平面,设中面上点A到A'的距离为Z，变形后,A点有挠度W, 同时发生弯曲， 曲面沿x方向的倾角为xw, 根据法线假定,则A'点沿x方向的位移: xwzu (负号为方向与x相反) 同理取zy 0平面得： ywzv (4-1-1) ③ Z平面的应变分量和曲、扭率 基本假定，由于0xyzxz, 故板内任意点的应变与平面问题相同:...