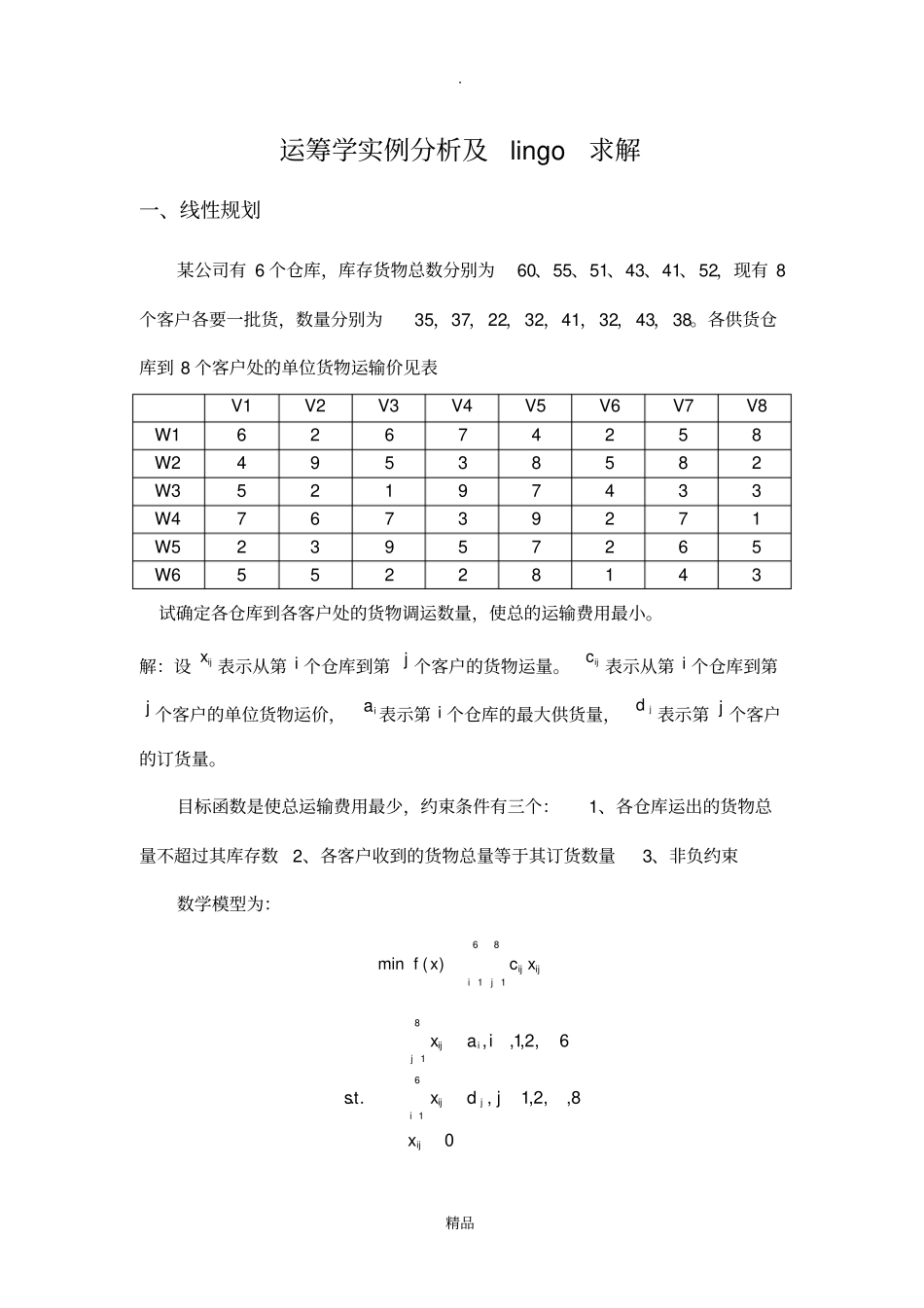
. 精品运筹学实例分析及lingo求解一、线性规划某公司有 6 个仓库,库存货物总数分别为60、55、51、43、41、52,现有 8个客户各要一批货,数量分别为35,37,22,32,41,32,43,38。各供货仓库到 8 个客户处的单位货物运输价见表V1V2V3V4V5V6V7V8W162674258W249538582W352197433W476739271W523957265W655228143试确定各仓库到各客户处的货物调运数量,使总的运输费用最小。解:设ijx 表示从第 i 个仓库到第 j 个客户的货物运量。ijc 表示从第 i 个仓库到第j 个客户的单位货物运价,ia 表示第 i 个仓库的最大供货量,jd 表示第 j 个客户的订货量。目标函数是使总运输费用最少,约束条件有三个:1、各仓库运出的货物总量不超过其库存数2、各客户收到的货物总量等于其订货数量3、非负约束数学模型为:6181)(minijijij xcxf08,,2,1,6,2,1,,..6181ijjiijijijxjdxiaxts. 精品编程如下:model:Sets:Wh/w1..w6/:ai;Vd/v1..v8/:dj;links(wh,vd):c,x;endsetsData: ai=60,55,51,43,41,52;dj=35,37,22,32,41,32,43,38;c=6,2,6,7,4,2,5,9 4,9,5,3,8,5,8,2 5,2,1,9,7,4,3,3 7,6,7,3,9,2,7,1 2,3,9,5,7,2,6,5 5,5,2,2,8,1,4,3;EnddataMin=@sum(links(i,j):c(i,j)*x(i,j));@for(wh(i):@sum(vd(j):x(i,j))<=ai(i));@for(vd(j):@sum(wh(i):x(i,j))=dj(j));end Global optimal solution found.. 精品 Objective value: 664.0000 Total solver iterations: 0 Variable Value Reduced Cost AI( W1) 60.00000 0.000000 AI( W2) 55.00000 0.000000 AI( W3) 51.00000 0.000000 AI( W4) 43.00000 0.000000 AI( W5) 41.00000 0.000000 AI( W6) 52.00000 0.000000 DJ( V1) 35.00000 0.000000 DJ( V2) 37.00000 0.000000 DJ( V3) 22.00000 0.000000 DJ( V4) 32.00000 0.000000 DJ( V5) 41.00000 0.000000 DJ( V6) 32.00000 0.000000 DJ( V7) 43.00000 0.000000 DJ( V8) 38.00000 0.000000 C( W1, V1) 6.000000 0.000000 C( W1, V2) 2.000000 0.000000 C( W1, V3) 6.000000 0.000000 C( W1, V4) 7.000000 0.000000. 精品 C( W1, V5) 4.000000 0.000000 C( W1, V6) 2.000000 0.000000 C( W1, V7) 5.000000 0.000000 C( W1, V8) 9.000000 0.000000 C( W2, V1) 4.000000 0.000000 C( W2, V2) 9.000000 0.000000 C( W...