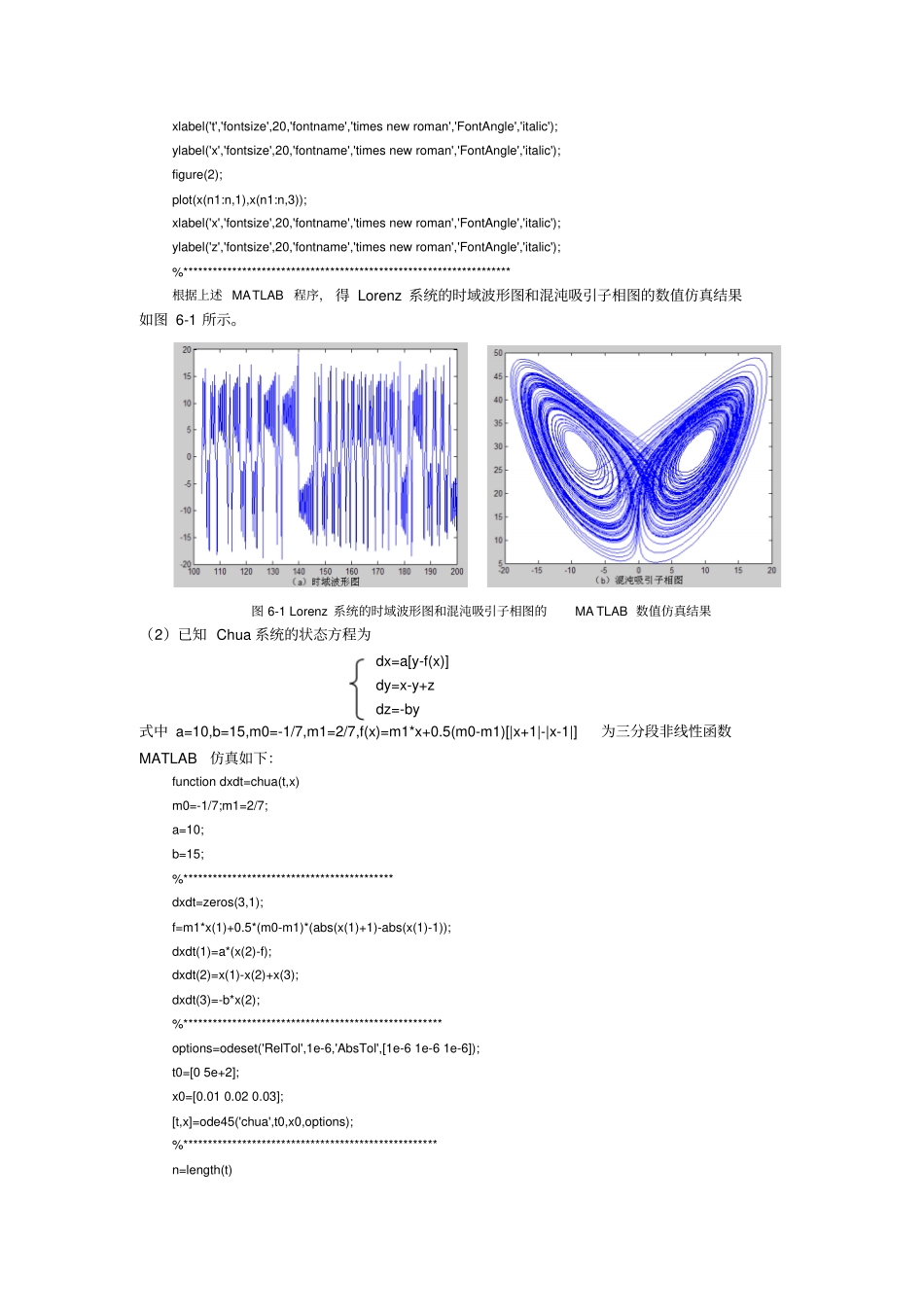
第 6 章 连续时间混沌系统本章讨论连续时间混沌系统的基本特点与分析方法,主要包括混沌数值仿真和硬件实验方法简介、 混沌系数平衡点的计算、平衡点的分类与性质、相空间中的轨道、几类典型连续混沌系统的介绍、混沌机理的分析方法、用特征向量空间法寻找异宿轨道、Lorenz 系统及混沌机理定性分析、Lorenz 映射、 Poincare 截面、 Chua 系统及其混沌机理定性分析、时间序列与相空间重构等内容。6.1 混沌数值仿真和硬件实验方法简介混沌的数值仿真主要包括MATLAB编程、 SIMULINK模块构建、 EWB 仿真以及其他一些相关的软件仿真或数值计算等方法,从而获取混沌吸引子的相图、时域波形图、 李氏指数、分叉图和功率谱等。混沌的硬件实验主要包括模拟/数字电路设计与硬件实验、现场可编程门阵列器件(FPGA)、数字信号处理器(DSP)等硬件实现方法来产生混沌信号。本节仅对各种数值仿真方法作简单介绍。1) 混沌系统的MATLAB数值仿真该方法主要根据混沌系统的状态方程来编写MA TLAB 程序。现举二例来说明这种编程方法。(1)已知 Lorenz 系统的状态方程为dx/dt=-a(x-y) dy/dt=bx-xz-y dz/dt=-cz+xy 式中 a=10,b=30,c=8/3 。MATLAB仿真程序如下:>> %************************************************** Function dxdt=lorenz(t,x) %除符号 dxdt 外,还可用其他编程者习惯的有意义的符号A=10; B=30; C=8/3; dxdt=zeros(3,1); dxdt(1)=-A*(x(1)-x(2)); dxdt(2)=B*x(1)-x(1).*x(3)-x(2); dxdt(3)=x(1)*x(2)-C*x(3); %************************************************* options=odeset('RelTol',1e-6,'AbsTol',[ 1e-6 1e-6 1e-6]); t0=[0 200]; x0=[0.02,0.01,0.03]; [t,x]=ode45('lorenz',t0,x0,options); %************************************************** n=length(t) n1=round(n/2) %n1=1; %************************************************** figure(1); plot(t(n1:n,1),x(n1:n,1)); xlabel('t','fontsize',20,'fontname','times new roman','FontAngle','italic'); ylabel('x','fontsize',20,'fontname','times new roman','FontAngle','italic'); figure(2); plot(x(n1:n,1),x(n1:n,3)); xlabel('x','fontsize',20,'fontname','times new roman','FontAngle','italic'); ylabel('z','fontsize',20,'fontname','times new roman','FontAngle','italic'); %***********...