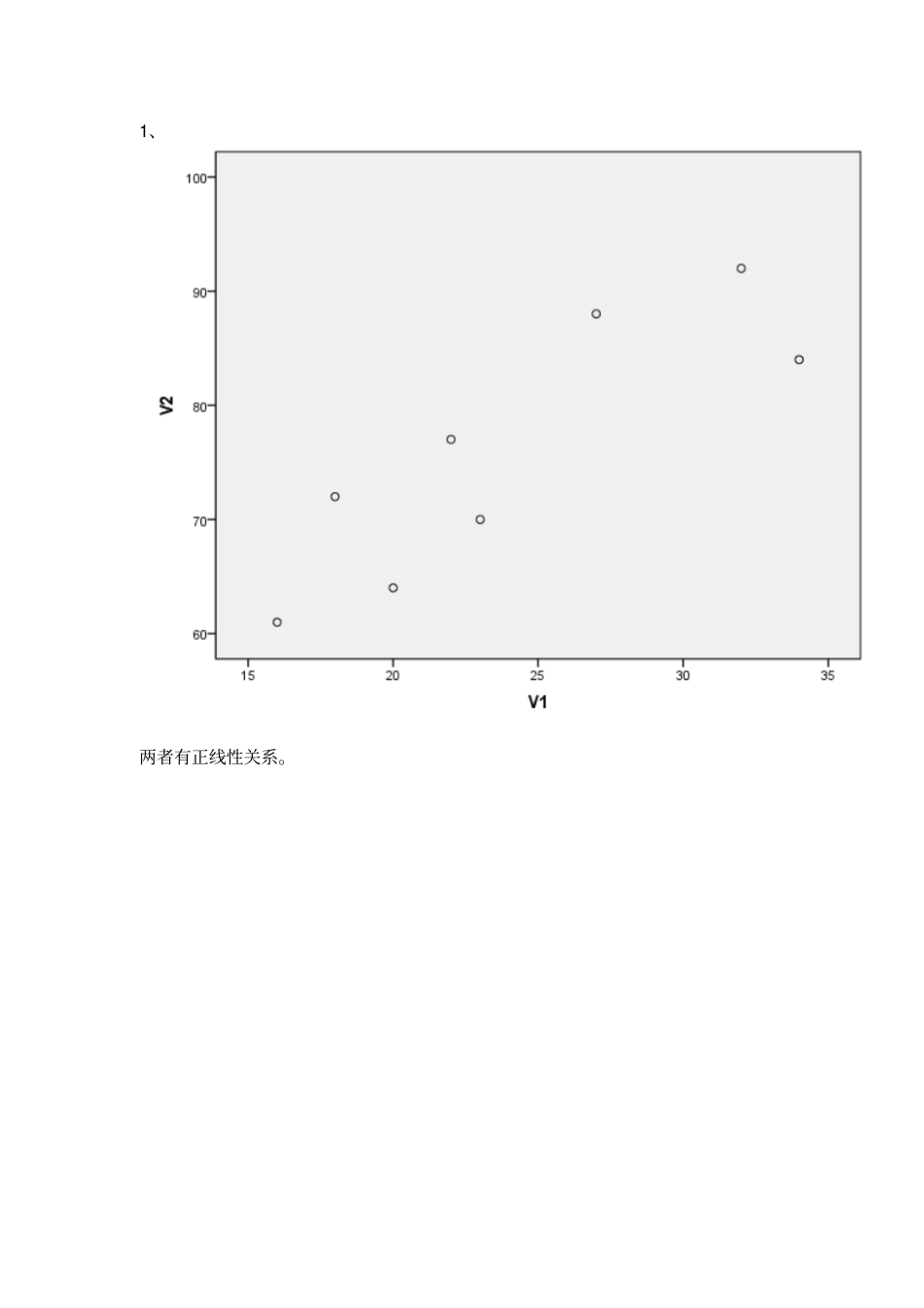
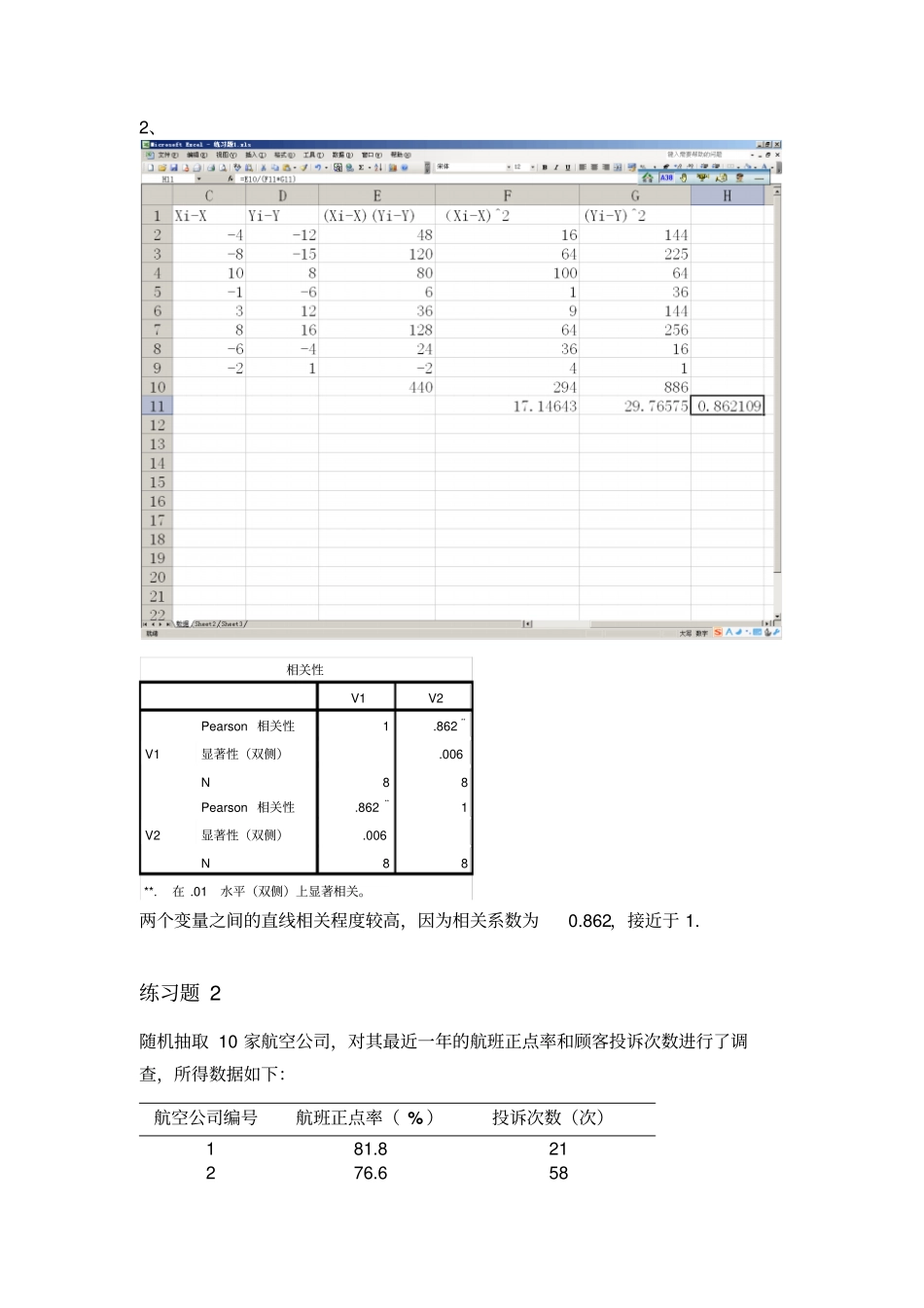
实验三 练习题练习题 1 学生在期末考试之前用于复习的时间(单位:h)和考试分数(单位:分)之间是否有关系?为研究这一问题,一位研究者抽取了由8 名学生构成的一个随机样本,得到的数据如下:复习时间 x 20 16 34 23 27 32 18 22 考试分数 y 64 61 84 70 88 92 72 77 要求:1. 绘制复习时间和考试分数的散点图,判断二者之间的关系形态。2. 计算相关系数,说明两个变量之间的关系强度。答:1、两者有正线性关系。2、相关性V1 V2 V1 Pearson 相关性1 .862**显著性(双侧).006 N 8 8 V2 Pearson 相关性.862**1 显著性(双侧).006 N 8 8 **. 在 .01 水平(双侧)上显著相关。两个变量之间的直线相关程度较高,因为相关系数为0.862,接近于 1. 练习题 2 随机抽取 10 家航空公司,对其最近一年的航班正点率和顾客投诉次数进行了调查,所得数据如下:航空公司编号航班正点率( % )投诉次数(次)1 81.8 21 2 76.6 58 3 76.6 85 4 75.7 68 5 73.8 74 6 72.2 93 7 71.2 72 8 70.8 122 9 91.4 18 10 68.5 125 要求:1. 绘制散点图,说明二者之间的关系形态。2. 用航班正点率作自变量,顾客投诉次数作因变量,求出估计的回归方程,并解释回归系数的意义。x 每变化一个单位时,影响 y 平均变动的数量3. 检验回归系数的显著性(α =0.05)。4. 如果航班正点率为80%,估计顾客投诉次数。5. 求航班正点率为 80%时,顾客投诉次数95%的置信区间和预测区间。答: 1、两者之间的关系:负线性相关2、模型汇总模型R R 方调整 R 方标准 估计的误差1 .869a.755 .724 18.887 a. 预测变量 : (常量 ), 航班正点率( %)。系数a模型非标准化系数标准系数t Sig. B 标准 误差试用版1 (常量 ) 430.189 72.155 5.962 .000 航班正点率( %)-4.701 .948 -.869 -4.959 .001 a. 因变量 : 投诉次数(次)回归方程: Y=430.189-4.701X+ξ回归系数的意义:系数小于0,说明航班正点率和投诉次数成负相关. 3、Anovaa模型平方和df 均方F Sig. 1 回归8772.584 1 8772.584 24.592 .001b残差2853.816 8 356.727 总计11626.400 9 a. 因变量 : 投诉次数(次)b. 预测变量 : (常量 ), 航班正点率( %)。回归系数的显著性概率为0.001,因此,线性关系显著。4、当 X=0.8时,Y=430.189-4.701X=54.109 5、置信区间:( 37.65953...