人教版高中数学正弦函数+余弦函数图像专题复习

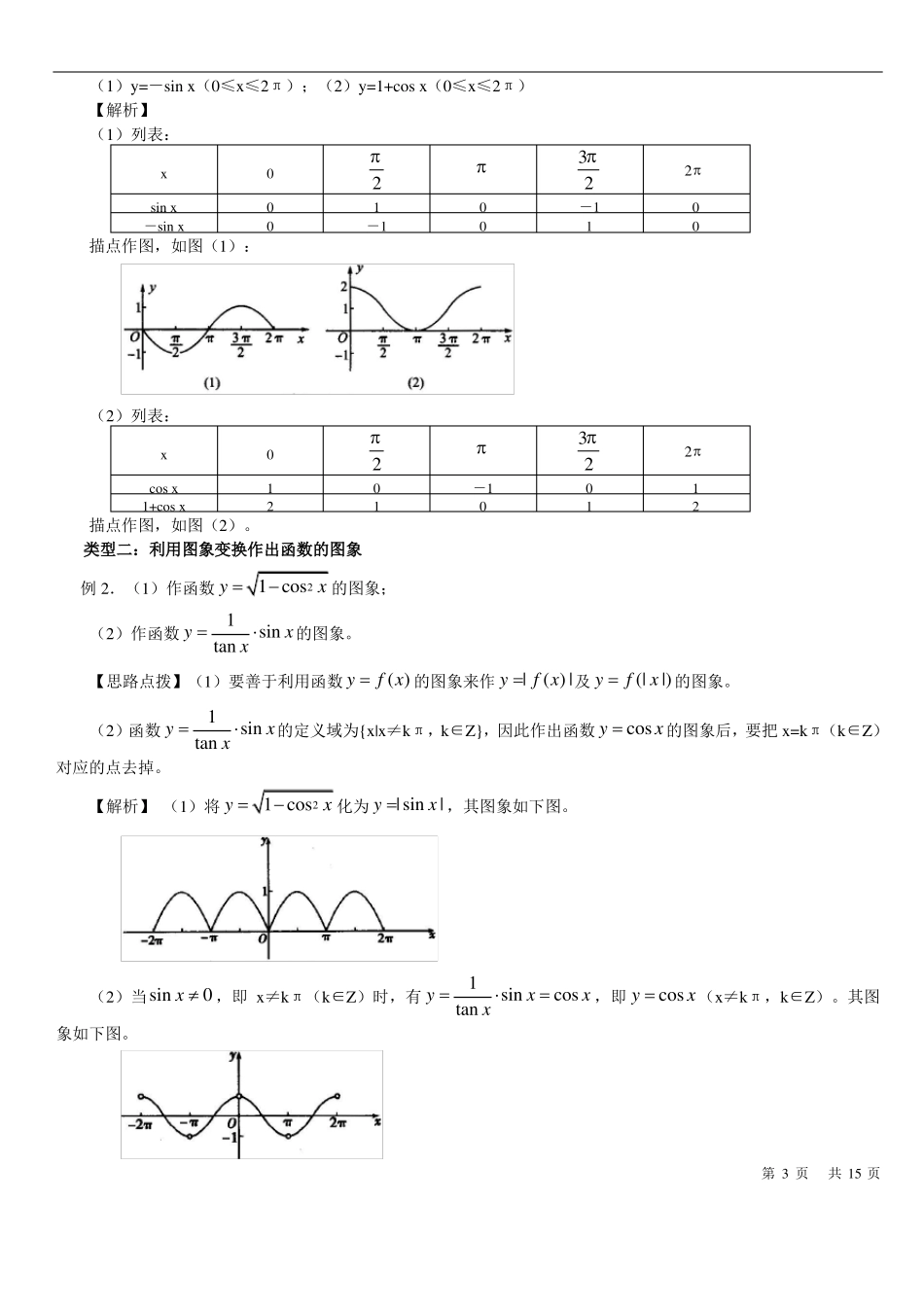
正弦函数、余弦函数的图象【要点梳理】要点一：正弦函数、余弦函数图象的画法1．描点法：按照列表、描点、连线三步法作出正弦函数、余弦函数图象的方法。2．几何法利用三角函数线作出正弦函数和余弦函数在[0,2]内的图象，再通过平移得到 y  sin x 和 y  cos x 的图象。3．五点法先描出正弦曲线和余弦曲线的波峰、波谷和三个平衡位置这五个点，再利用光滑曲线把这五点连接起来，就得到正弦曲线和余弦曲线在一个周期内的图象。在确定正弦函数 y  sin x 在[0,2]上的图象形状时，起关键作用的五个点是(0,0),(要点诠释：（1）熟记正弦函数、余弦函数图象起关键作用的五点。（2）若 x R ，可先作出正弦函数、余弦函数在[0,2]上的图象，然后通过左、右平移可得到 y  sin x 和 y  cos x的图象。（3）由诱导公式 y  cos x  sin(x 单位长度得到。要点二：正弦曲线、余弦曲线（1）定义：正弦函数 y  sin x(x R) 和余弦函数 y  cos x(x R) 的图象分别叫做正弦曲线和余弦曲线。（2）图象3,1),(,0),( ,1),(2,0)222) ，故 y  cos x 的图象也可以将 y  sin x 的图象上所有点向左平移个2要点诠释：（1）由正弦曲线和余弦曲线可以研究正弦函数、余弦函数的性质。（2）运用数形结合的思想研究与正弦函数、余弦函数有关的问题，如x0,2 ，方程lg x  sin x 根的个数。要点三：函数图象的变换图象变换就是以正弦函数、余弦函数的图象为基础通过对称、平移而得到。第 1 页共 15 页y  sin x  y  sin(x )  y  Asin(x )【典型例题】类型一：“五点法”作正、余弦函数的图象例 1．用五点法作出下列函数的图象。（1） y  2 sin x ， x[0,2 ]；（2） y  cos x  6  ， x   11 ,。66 【思路点拨】（1）取[0,2 ] 上五个关键的点（0，2）、（3，1）、( ,2) 、(,3) 、（2 ，2）。（2）取22  11 ,上五个关键的点。66【解析】（1）找出五点，列表如下：x0022110232－13202u  sin xy=2－u描点作图（如下图）。（2）找出五点，列表如下：u  x x606123056－13243021161y=cos u描点作图（如下图）。【总结升华】在精确度要求不太高时，我们常常先找出这五个关...