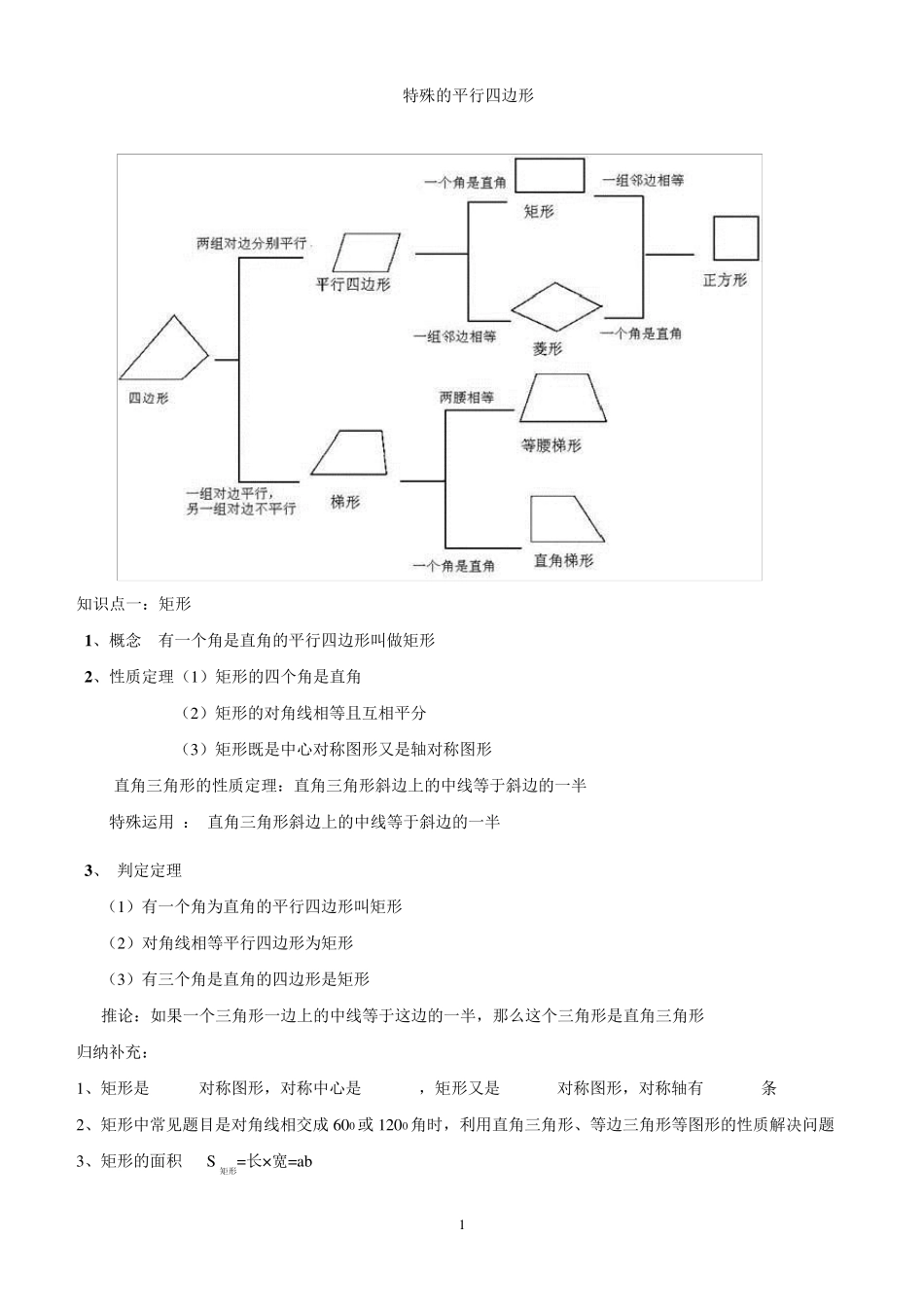
1 特殊的平行四边形 知识点一:矩形 1 、概念 有一个角是直角的平行四边形叫做矩形 2 、性质定理(1)矩形的四个角是直角 (2)矩形的对角线相等且互相平分 (3)矩形既是中心对称图形又是轴对称图形 直角三角形的性质定理:直角三角形斜边上的中线等于斜边的一半 特殊运用 : 直角三角形斜边上的中线等于斜边的一半 3 、 判定定理 (1)有一个角为直角的平行四边形叫矩形 (2)对角线相等平行四边形为矩形 (3)有三个角是直角的四边形是矩形 推论:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形 归纳补充: 1、矩形是 对称图形,对称中心是 ,矩形又是 对称图形,对称轴有 条 2、矩形中常见题目是对角线相交成 600 或 1200 角时,利用直角三角形、等边三角形等图形的性质解决问题 3、矩形的面积 S矩形=长×宽=ab 2 知识点二: 菱形 1、定义:一组邻边相等的平行四边形叫做菱形 2、性质定理: (1 )菱形的四条边都相等 (2 )菱形的对角线互相垂直平分,且每条对角线平分一组对角 (3 )菱形是轴对称图形,两条对角线所在的直线是都是它的对称轴 菱形是中心对称图形,对角线的交点是它的对称中心 2、 判定定理: (1 )一组邻边相等的平行四边形是菱形 (2 )对角线互相垂直的平行四边形是菱形 (3 )四条边都相等的四边形是菱形 ※注意:对角线互相垂直的四边形不一定是菱形,对角线互相垂直平分的四边形才是菱形 归纳补充: 1 、菱形被对角线分成四个全等的 三角形和两对全等的 三角形 2 、菱形的面积可以用平行四边形面积公式计算,也可以用两对角线积的 来计算 3 、菱形常见题目是内角为 1 2 0 0 或 6 0 0 时,利用等边三角形或直角三角形的相关知识解决题目 知识点三:正方形 1、定义:有一组邻边相等的矩形叫正方形 2、性质定理 (1 )正方形的四条边都相等,四个角是直角。 (2 )正方形的两条对角线相等且互相垂直平分,每一组对角线平分一组对角 (3 )正方形既是中心对称图形,又是轴对称图形 3、判定定理 (1 )有一组邻边相等的矩形是正方形 (2 )对角线相互垂直的矩形是正方形 (3 )对角线相等的菱形是正方形 (4 )有一个角是直角的菱形是正方形 方法总结: (1)判定一个四边形是正方形的主要依据是定义,途径有两种: 先证它是矩形,再证有一组邻边相等。 先证它是菱形,再证有一个角是直角。 3 ...