状态空间与simulink仿真

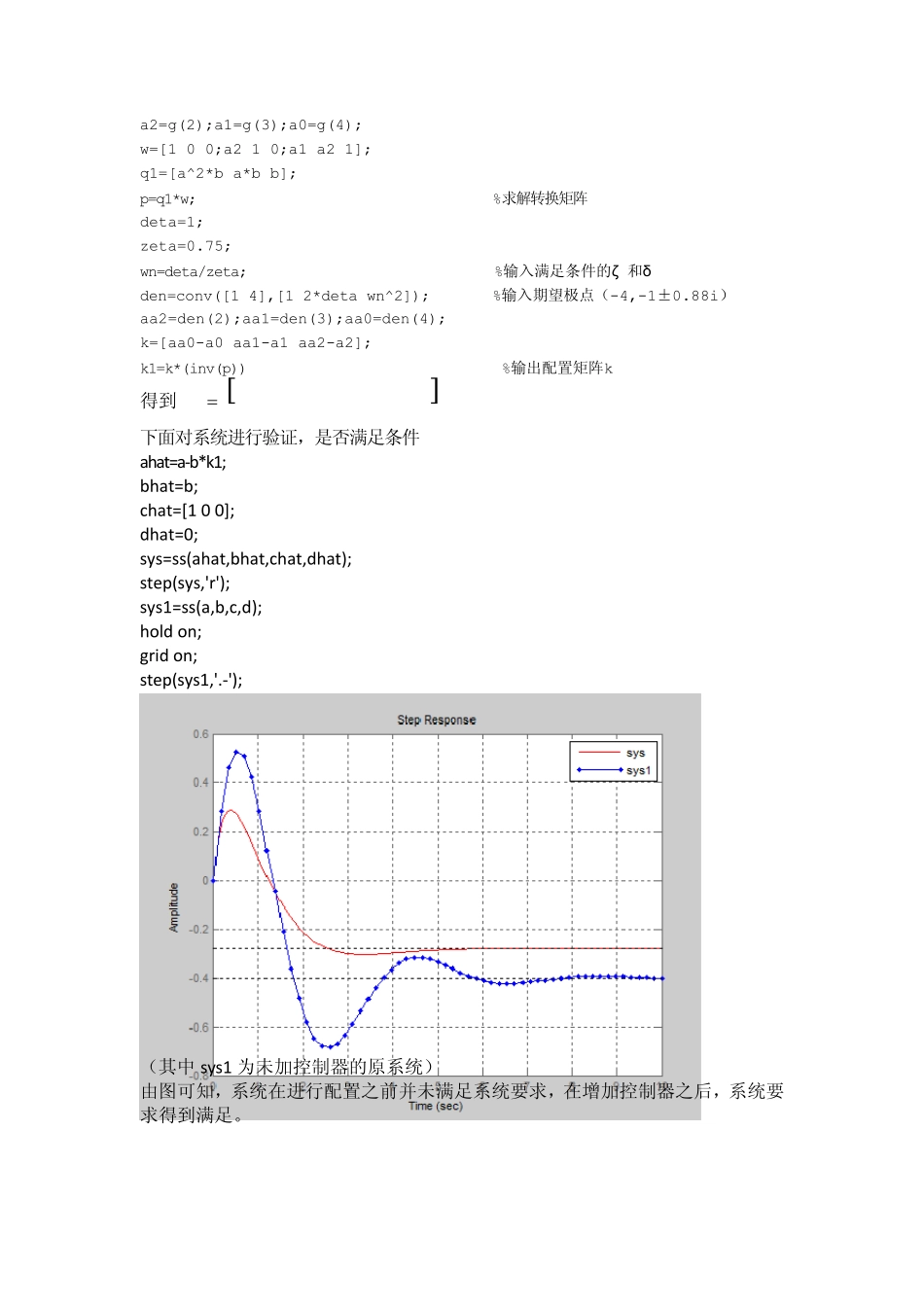
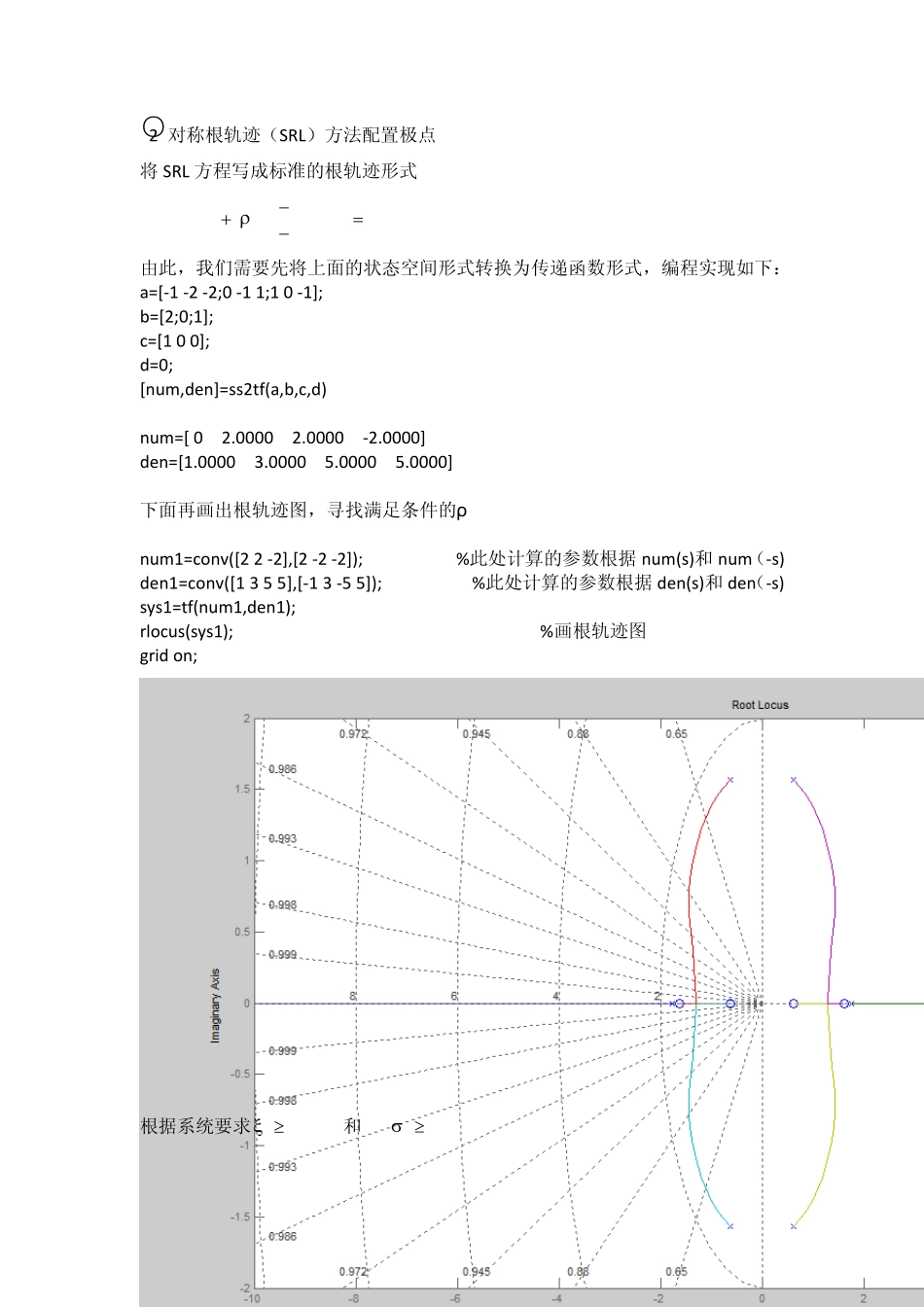
考虑以下系统 uxX102101110221 xy001 对系统设计一个状态反馈控制器使得闭环阶跃响应的超调量小于5%，且在稳态值1%范围的调节时间小于4.6S。 ○1 主导二阶极点方法配置极点 分析： 超调量小于5%，即 %521e 算得 69.0 稳态值1%范围的调节时间小于4.6S，即 6.46.4st 1 下面首先对系统的能控性进行判断，以编程方式实现 a=[-1 -2 -2;0 -1 1;1 0 -1]; b=[2;0;1]; %输入a，b矩阵 q=[b a*b a^2*b] rank(q) 计算结果为 511010042q q 的秩为 3 因此该系统为完全能控型系统，在满足系统要求的前提下，理论上能任意配置期望极点 下面根据具体的求解思路进行编程求解反馈控制器k g=poly(a); %求原系统的特征方程 a2=g(2);a1=g(3);a0=g(4); w=[1 0 0;a2 1 0;a1 a2 1]; q1=[a^2*b a*b b]; p=q1*w; %求解转换矩阵 deta=1; zeta=0.75; wn=deta/zeta; %输入满足条件的ζ 和δ den=conv([1 4],[1 2*deta wn^2]); %输入期望极点（-4,-1±0.88i） aa2=den(2);aa1=den(3);aa0=den(4); k=[aa0-a0 aa1-a1 aa2-a2]; k1=k*(inv(p)) %输出配置矩阵k 得到0444.06444.14778.11k 下面对系统进行验证，是否满足条件 ahat=a-b*k1; bhat=b; chat=[1 0 0]; dhat=0; sys=ss(ahat,bhat,chat,dhat); step(sys,'r'); sys1=ss(a,b,c,d); hold on; grid on; step(sys1,'.-'); （其中 sys1 为未加控制器的原系统） 由图可知，系统在进行配置之前并未满足系统要求，在增加控制器之后，系统要求得到满足。 ○2 对称根轨迹（SRL）方法配置极点 将 SRL 方程写成标准的根轨迹形式 0)()()()(1sDsDsNsN 由此，我们需要先将上面的状态空间形式转换为传递函数形式，编程实现如下： a=[-1 -2 -2;0 -1 1;1 0 -1]; b=[2;0;1]; c=[1 0 0]; d=0; [num,den]=ss2tf(a,b,c,d) num=[ 0 2.0000 2.0000 -2.0000] den=[1.0000 3.0000 5.0000 5.0000] 下面再画出根轨迹图，寻找满足条件的ρ num1=conv([2 2 -2],[2 -2 -2]); %此处计算的参数根据 num(s)和 num（-s) den1=conv([1 3 5 5],[-1 3 -5 5]); %此处计算的参数根据 den(s)和 den（-s) sys1=tf(num1,den1); rlocus(sys1); %画根轨迹图 grid on; 根据系统要求69.0...