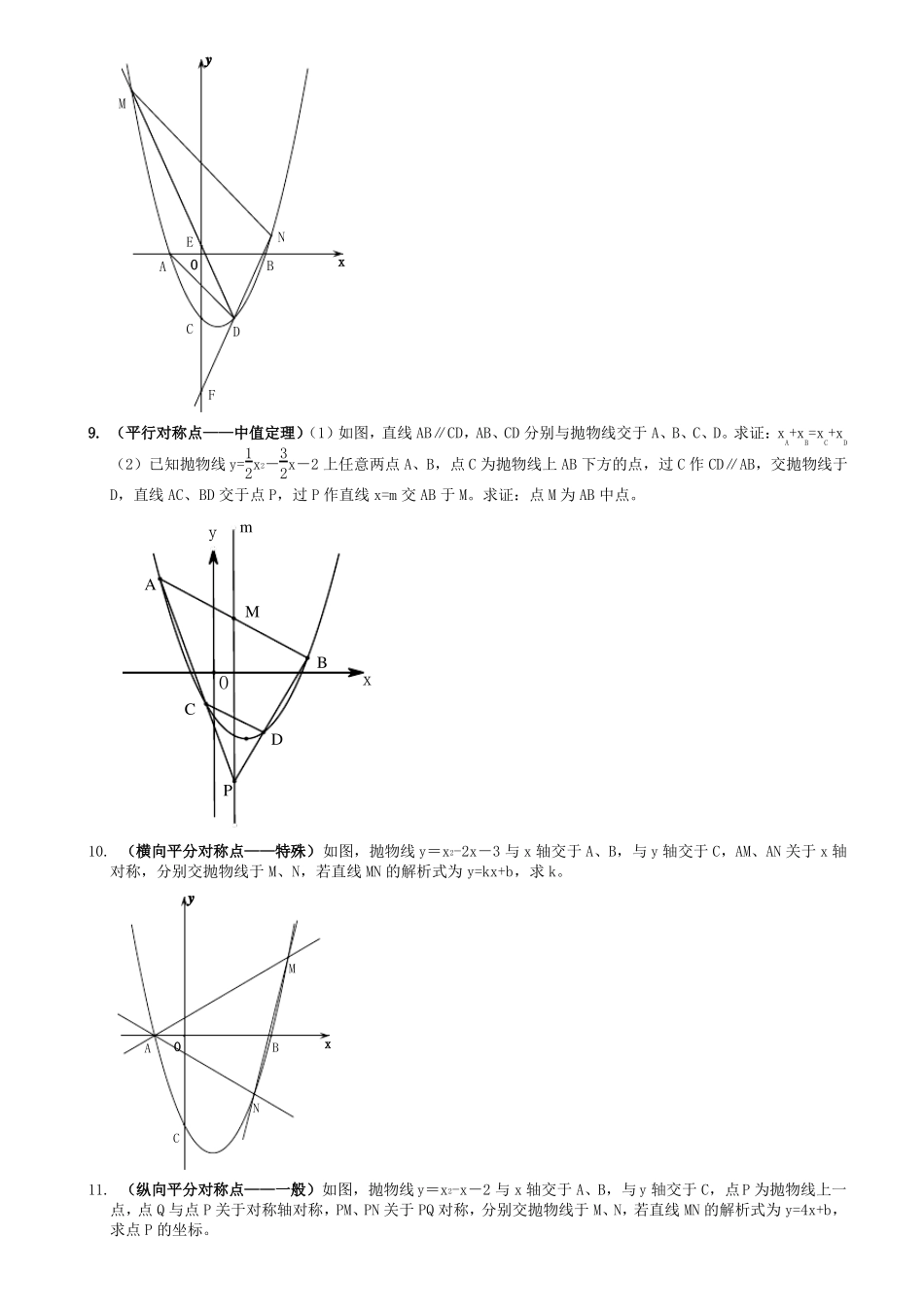
初中抛物线常见结论汇总(教师版)1. (唯一交点或最值)2(1)已知抛物线 y=x -2x-3,过点 D(0,-4)求与抛物线有且只有一个公共点的直线的解析式。 (判别式)2(2)已知抛物线 y=x -2x-3,在第四象限的抛物线上求点 P,使四边形 ACPB 的面积最大。yyAOBxAOBxC2.(焦点—准线:顶点上下C112个单位)已知抛物线 y= x -x+1,直线过点 P(1,1)与抛物线交于 A、B。过 A、4a2B 分别作 x 轴的垂线,垂足分别为 M、N。(1)连 PM、PN,求证:△PMN 为直角三角形;11(2)①求证:AB=AM+BN;②求+的值。APBP(3)已知点 D(1,0),求证:DP 经过△ABD 的内心。yAPCMOAyBxPCMODBxNN1233.如图,抛物线 y= x ﹣x- 顶点为 D,对称轴上有一点 E(1,4),在抛物线上求点 P,使∠EPD=90°。22yEAOCBDx124. (定直角特殊点——特殊)已知抛物线 y= x ,过对称轴上 P 点的任意一条直线与抛物线的两交点 A、B 和 O 点2构成以 O 点为直角顶点的直角三角形,求 P 点坐标。(定点:顶点向上平移 1/a 个单位长度)yAPBOx25. (定直角特殊点——半特殊)如图:抛物线 y=ax +bx+c 与 x 轴交于 A、B,与 y 轴交于 C,交点 C 向上平移 t个单位长度到 D,过 D 作 EF∥AB,交抛物线于 E、F,∠ECF=90°。求 t 与 a 的关系。yEACDOBFx26. (定直角特殊点——一般)如图:抛物线 y=ax +bx+c 与 x 轴交于 A、B,与 y 轴交于 C,点 P(m,n)为抛物线上任意一点,过 D(0,n+t)作 EF∥AB,交抛物线于 E、F,∠EPF=90°。求 t 与 a 的关系。yEDFBPxACO127. (纵向平分对称点——特殊)已知抛物线 y= x ,过对称轴上 P 点的任意一条直线与抛物线的两交点为 A、B,2在对称轴负半轴上有点 Q(0,-2),且∠AQB 被对称轴平分,求 P 点坐标。yAPBOQx28. (纵向平分对称点——一般)如图,抛物线 y=x -x-2 与 x 轴交于 A、B,与 y 轴交于 C,点 D 和点 C 关于对称轴对称,MN∥AD,交抛物线于 M、N,直线 MD、ND 分别交 y 轴于 E、F。求证:CF=CE。yMEAOBNxCDF9. (平行对称点——中值定理)(1)如图,直线 AB∥CD,AB、CD 分别与抛物线交于 A、B、C、D。求证:xA+xB=xC+xD123(2)已知抛物线 y= x - x-2 上任意两点 A、B,点 C 为抛物线上 AB 下方的点,过 C 作 CD∥AB,交抛物线于22D,直线 AC、BD 交于点 P,过 P ...