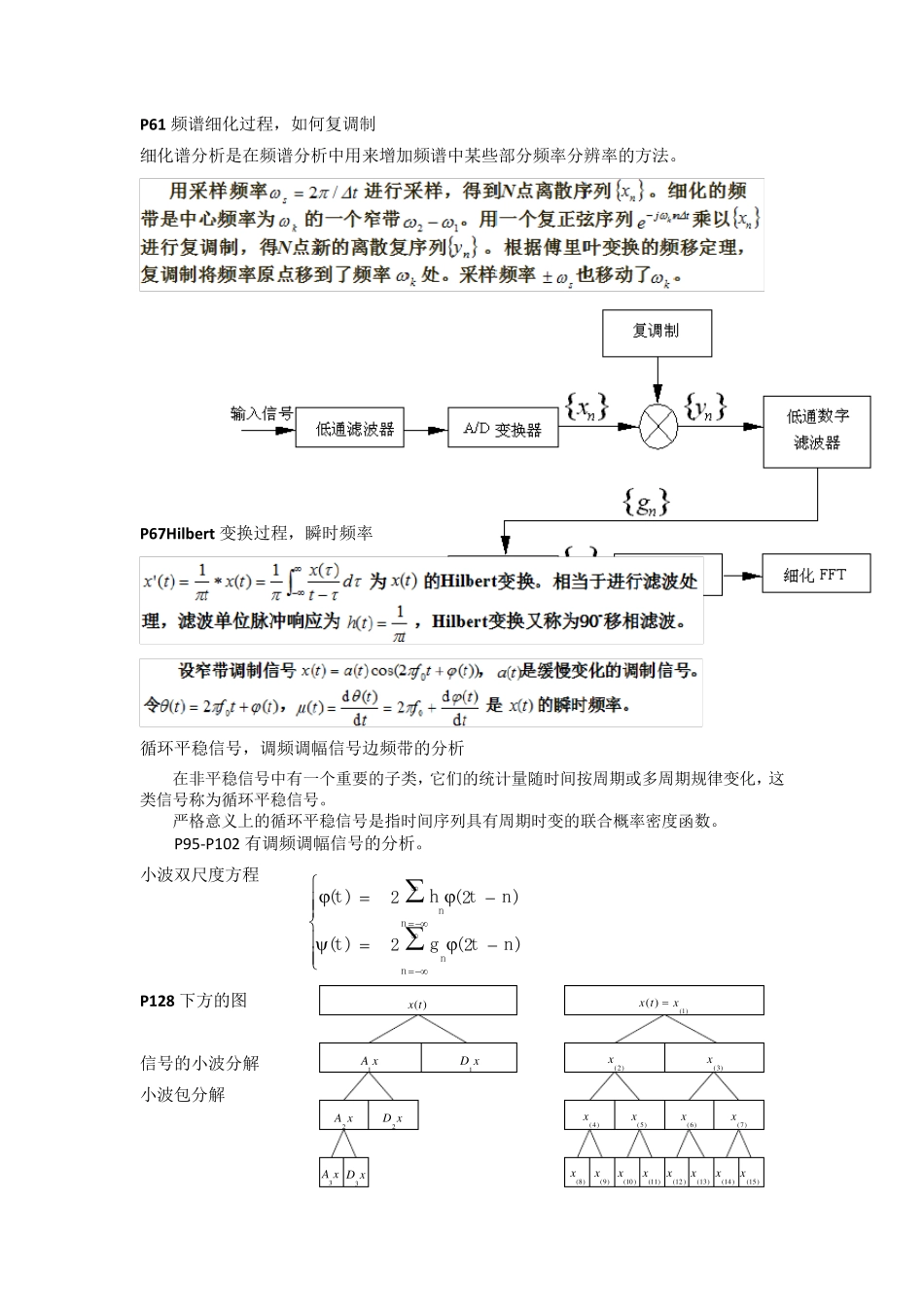
P29 采样、频率混叠，画图说明 将连续信号转换成离散的数字序列过程就是信号的采样
它包含了离散和量化两个主要步骤
若采样间隔Δt 太大，使得平移距离2π/Δt过小
移至各采样脉冲函数对应频域序列点上的频谱 X()就会有一部分相互重叠，如图虚线部分所示，由此造成离散信号的频谱与原信号频谱不一致，这种现象称为混叠
P33 列举时域参数（有量纲和无量纲），说明其意义与作用
有量纲参数指标包括方根幅值、平均幅值、均方幅值和峰值四种
无量纲参数指标包括了波形指标、峰值指标、脉冲指标和裕度指标
偏斜度指标 S 表示信号概率密度函数的中心偏离正态分布的程度，反映信号幅值分布相对其均值的不对称性
峭度指标 K 表示信号概率密度函数峰顶的陡峭程度，反映信号波形中的冲击分量的大小
P37～自相关互相关及作用（举例说明） 相关，就是指变量之间的线性联系或相互依赖关系
信号x(t)的自相关函数： 信号中的周期性分量在相应的自相关函数中不会衰减，且保持了原来的周期
因此，自相关函数可从被噪声干扰的信号中找出周期成分
在用噪声诊断机器运行状态时，正常机器噪声是由大量、无序、大小近似相等的随机成分叠加的结果，因此正常机器噪声具有较宽而均匀的频谱
当机器状态异常时，随机噪声中将出现有规则、周期性的信号，其幅度要比正常噪声的幅度大得多
依靠自相关函数就可在噪声中发现隐藏的周期分量，确定机器的缺陷所在
（如：自相关分析识别车床变速箱运行状态，确定存在缺陷轴的位置；确定信号周期
） 互相关函数： 互相关函数的周期与信号x(t)和y(t)的周期相同，同时保留了两个信号的相位差信息φ
可在噪音背景下提取有用信息；速度测量；板墙对声音的反射和衰减测量等
（如：利用互相关分析测定船舶的航速；探测地下水管的破损地点
P42） P51～蝶形算法 FFT 的基本思想是把长度为 2 的正整数次幂的
