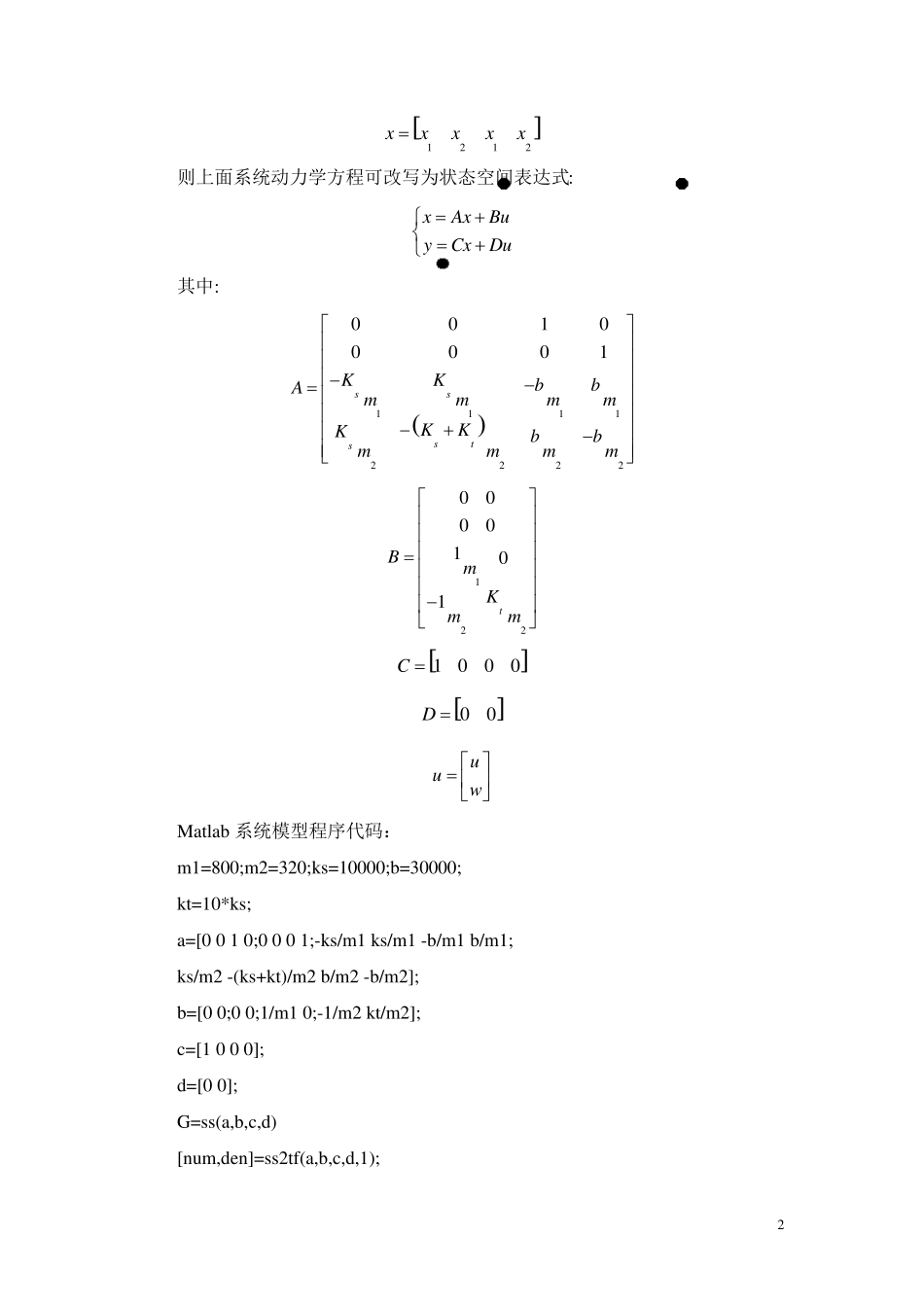
现代控制理论大作业 分析对象:汽车悬架系统 指导老师:*** 专 业:机械工程 * ***** 学 号:S******** 1 1.建模 悬架是车轮或车桥与汽车承载部分之间具有弹性的连接装置的总称,具有传递载荷、缓和冲击、衰减振动以及调节汽车行驶中的车身位置等作用。传统汽车悬驾系统是被动悬驾,其参数不能改变,无法控制其对不同路面激励的响应,因此对不同路面的适应性较差。为提高汽车的行驶平顺性、操纵稳定性和制动性等性能,人们开始用主动悬架系统来代替传统的被动悬架系统。主动悬架系统能根据路面的情况通过一个动力装置改变悬挂架的参数,改善汽车的各方面性能。 对悬驾系统进行仿真计算首先要建立悬驾系统动力学模型,随后对所建立的模型进行仿真分析。为了简化模型,取汽车的一个车轮的悬驾系统进行研究,该模型可简化为一维二自由度的弹簧阻尼质量系统,图 1 所示为该模型的模拟图。 图 1 悬架系统模型的模拟图 其中 u 为动力装置的作用力,w 为路面位移,x1 为车身位移,x2 为悬驾位移,用车身位移来度量车身的振动情况,并视为系统的输出。路面状况以 w 为尺度,并视为系统的一个干扰输入。当汽车从平面落入坑时,w 可用一个阶跃信号来模拟。u 为主动悬架的作用力,它是系统的控制量。 进行受力分析,由牛顿第二规律可得车身悬架系统的动力学方程为 : 1 121212212122sstm xKxxb xxum xKxxb xxuKwx 设系统状态变量为: 2 1212xxxxx 则上面系统动力学方程可改写为状态空间表达式: xAx Buy Cx Du 其中: 1111222200100001ssstsKKbbAmmmmKKKbbmmmm 1220000101tBmKmm 1000C 00D uuw Matlab 系统模型程序代码: m1=800;m2=320;ks=10000;b=30000; kt=10*ks; a=[0 0 1 0;0 0 0 1;-ks/m1 ks/m1 -b/m1 b/m1; ks/m2 -(ks+kt)/m2 b/m2 -b/m2]; b=[0 0;0 0;1/m1 0;-1/m2 kt/m2]; c=[1 0 0 0]; d=[0 0]; G=ss(a,b,c,d) [nu m,den]=ss2tf(a,b,c,d,1); 3 tfsy s=tf(nu m,den) eig(a) figu re(1) impu lse(G) figu re(2) step(G) 系统状态空间模型:: 系统传递函数: 系统矩阵特征值: 4 系统矩阵特征值都在左半平面,故系统稳定。 系统脉...