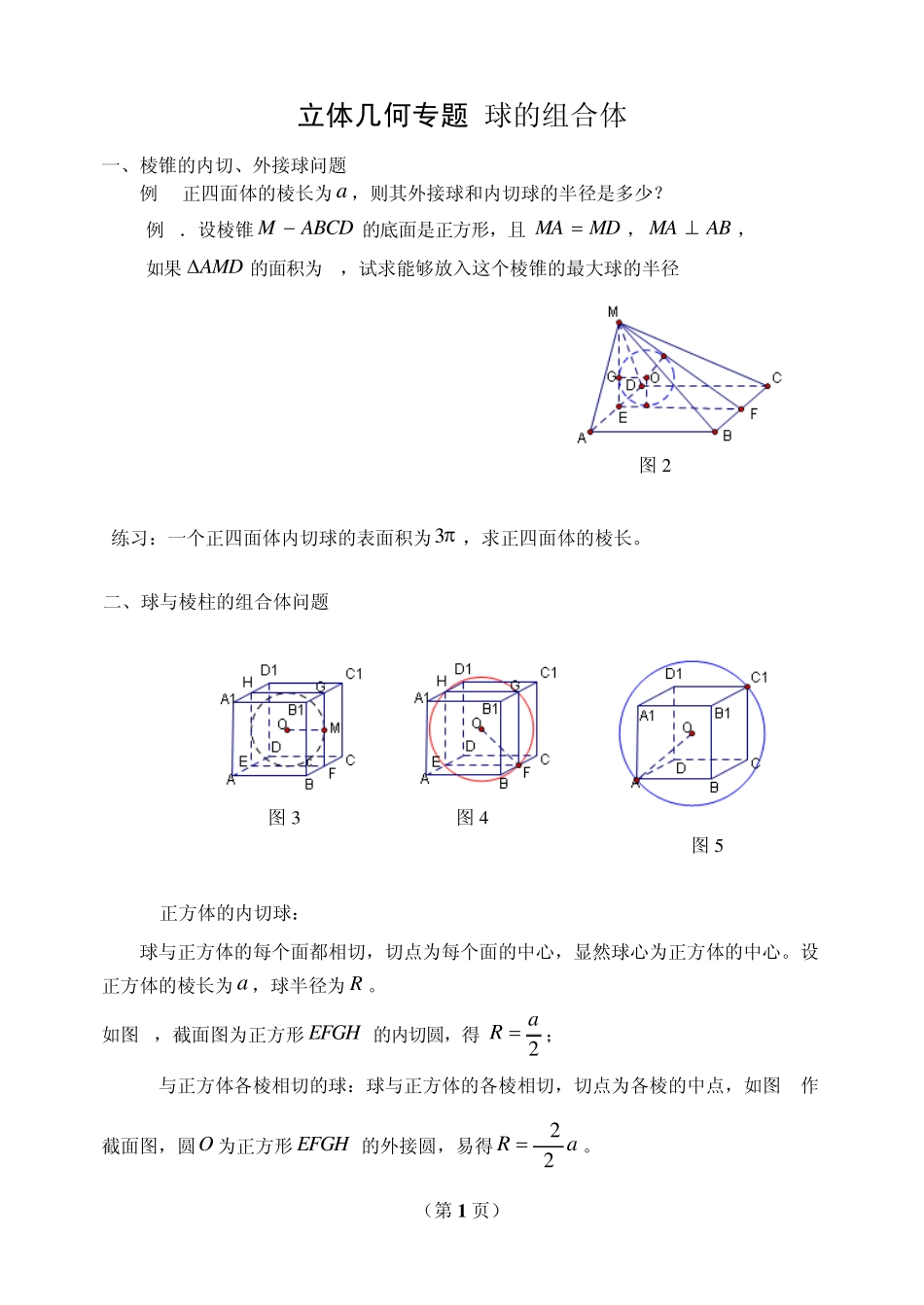
(第1 页) 立体几何专题:球的组合体 一、棱锥的内切、外接球问题 例 1.正四面体的棱长为 a,则其外接球和内切球的半径是多少? 例 2.设棱锥ABCDM 的底面是正方形,且MDMA ,ABMA , 如果AMD的面积为 1,试求能够放入这个棱锥的最大球的半径. 练习:一个正四面体内切球的表面积为 3,求正四面体的棱长。 二、球与棱柱的组合体问题 1.正方体的内切球: 球与正方体的每个面都相切,切点为每个面的中心,显然球心为正方体的中心。设正方体的棱长为 a,球半径为 R 。 如图 3,截面图为正方形 EFGH 的内切圆,得2aR ; 2.与正方体各棱相切的球:球与正方体的各棱相切,切点为各棱的中点,如图 4作截面图,圆O 为正方形 EFGH 的外接圆,易得aR22。 图 3 图 4 图 5 图 2 (第2 页) 3.正方体的外接球:正方体的八个顶点都在球面上,如图5,以对角面1AA 作截面图得,圆O 为矩形CCAA11的外接圆,易得aOAR231。 例3.在球面上有四个点P 、A 、B 、C .如果PA 、PB 、PC 两两互相垂直,且aPCPBPA,那么这个球的表面积是______. 练习:一棱长为a2的框架型正方体,内放一能充气吹胀的气球,求当球与正方体棱适好接触但又不至于变形时的球的体积。 4.构造直三角形,巧解正棱柱与球的组合问题 正棱柱的外接球,其球心定在上下底面中心连线的中点处,由球心、底面中心及底面一顶点构成的直角三角形便可得球半径。 例4.已知正三棱柱111CBAABC 的六个顶点在球1O 上,又知球2O 与此正三棱柱的5个面都相切,求球1O 与球2O 的体积之比与表面积之比。 练习:正四棱柱1111DCBAABCD 的各顶点都在半径为R 的球面上,求正四棱柱的侧面积的最大值。(答案为:224R ) 【点评】“内切”和“外接”等有关问题,首先要弄清几何体之间的相互关系,主要是指特殊的点、线、面之间关系,然后把相关的元素放到这些关系中解决问题,作出合适的截面图来确定有关元素间的数量关系,是解决这类问题的最佳途径。 图6 (第3 页) 练习题: 1、 已知三棱锥 PABC的四个顶点均在半径为 1的球面上,且满足 PA 、PB 、PC 两两垂直,当PC AB 取最大值时,三棱锥OPAB(O 为球心)的高为_____。 2、 在平行四边形 ABCD 中,0AB BD ,222||||6ABBD,若将ABD沿 BD 折成直二面角ABDC,则三棱锥 ABCD外接球的表面积是____。 3、 在四面体 ABCD中,4ABCD...