理力典型习题

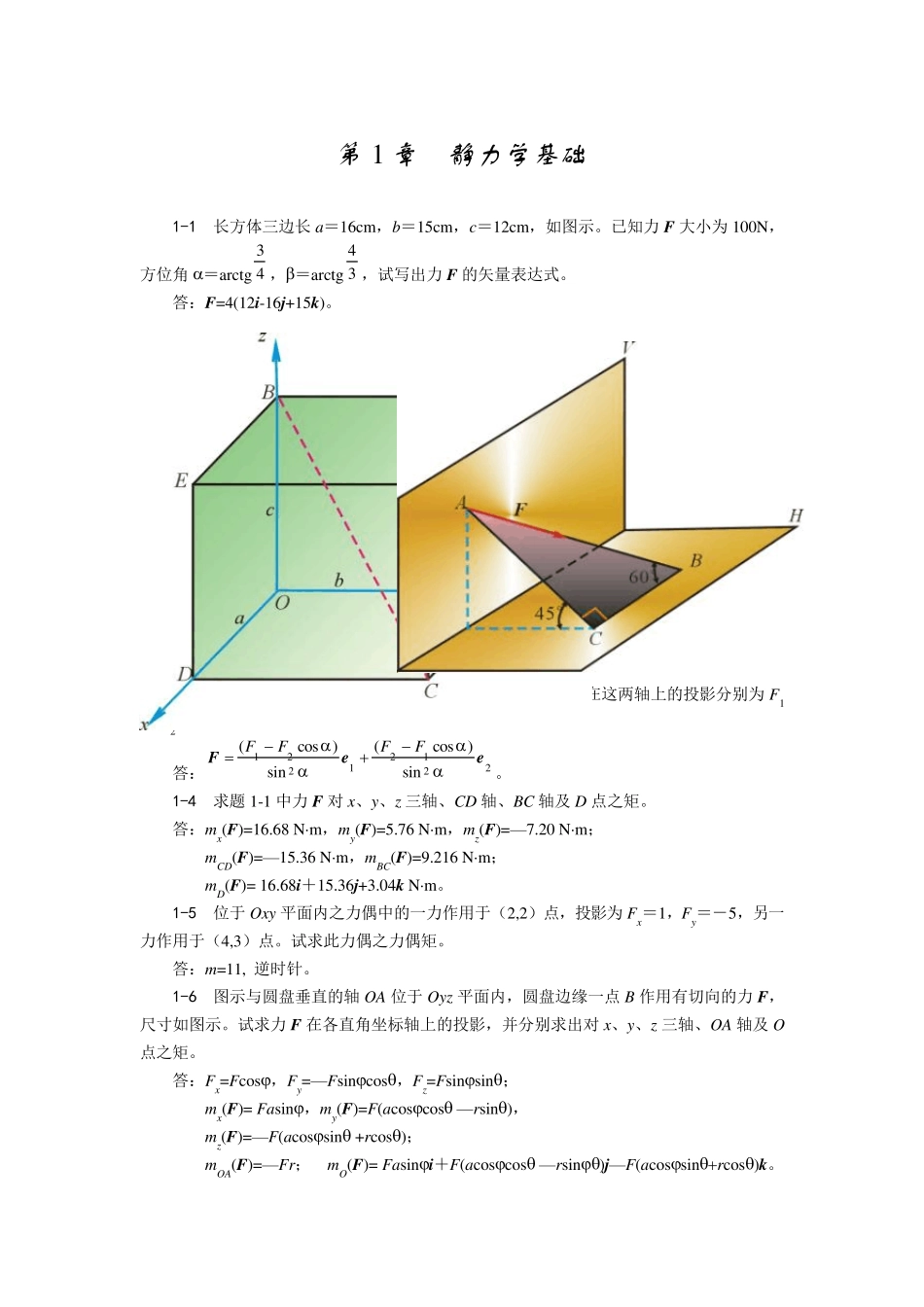
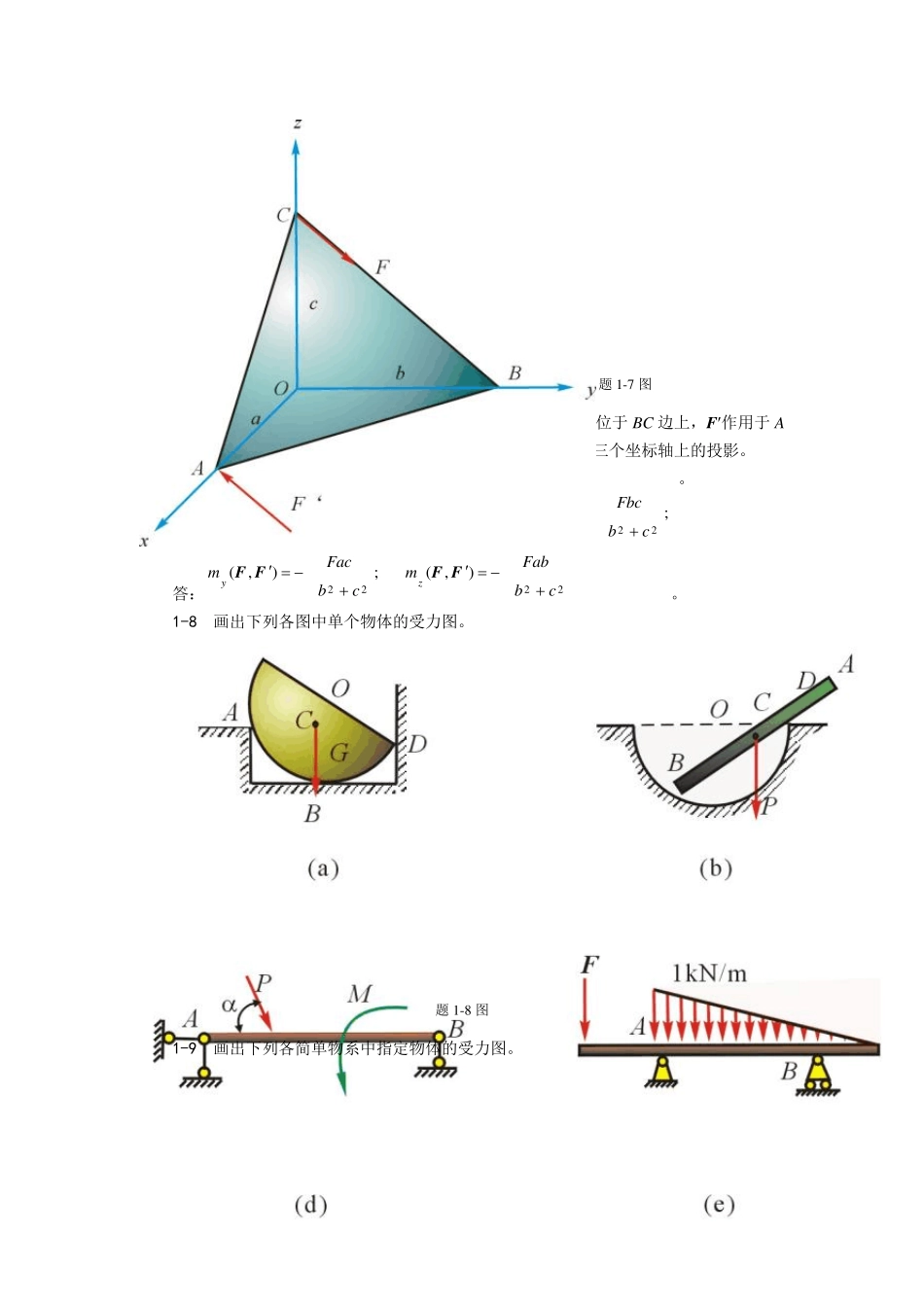
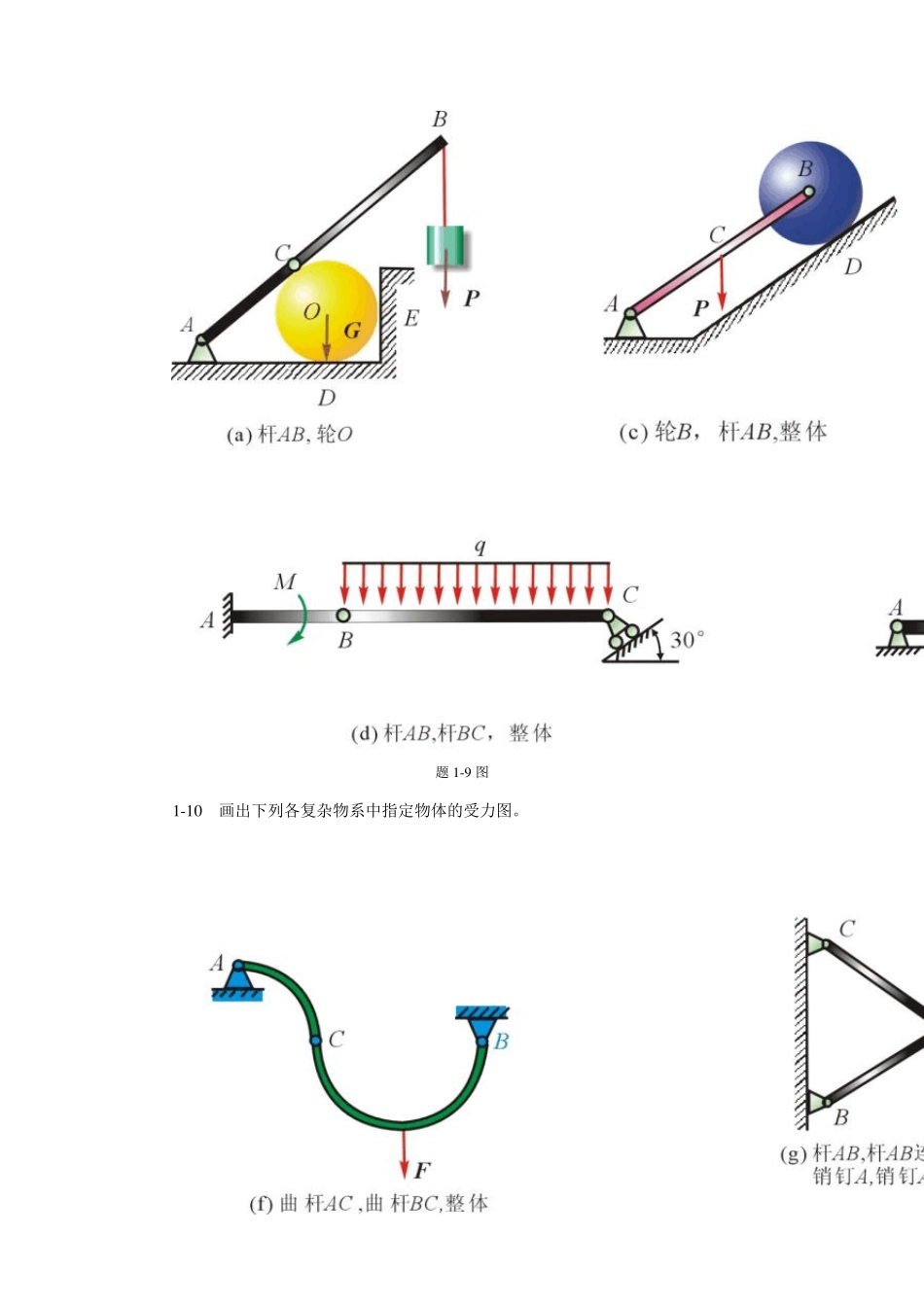
第1 章 静力学基础 1-1 长方体三边长a＝16cm，b＝15cm，c＝12cm，如图示。已知力F 大小为100N，方位角＝arctg 43，＝arctg 34，试写出力F 的矢量表达式。 答：F=4(12i-16j+15k )。 题1-1 图 题1-2 图 1-2 V、H 两平面互相垂直，平面ABC 与平面H 成45，ABC 为直角三角形。求力F在平面V、H 上的投影。 答：SH= SV=0.791S。 1-3 两相交轴夹角为（≠0），位于两轴平面内的力F 在这两轴上的投影分别为F1和 F2。试写出F 的矢量式。 答：22121221sin)cos(sin)cos(eeFFFFF。 1-4 求题1-1 中力F 对 x、y、z 三轴、CD 轴、BC 轴及 D 点之矩。 答：mx(F)=16.68 Nm，my(F)=5.76 Nm，mz(F)=—7.20 Nm； mCD(F)=—15.36 Nm，mBC(F)=9.216 Nm； mD(F)= 16.68i＋15.36j+3.04k Nm。 1-5 位于 Oxy 平面内之力偶中的一力作用于（2,2）点，投影为Fx＝1，Fy＝－5，另一力作用于（4,3）点。试求此力偶之力偶矩。 答：m=11, 逆时针。 1-6 图示与圆盘垂直的轴OA 位于 Oyz 平面内，圆盘边缘一点 B 作用有切向的力F，尺寸如图示。试求力F 在各直角坐标轴上的投影，并分别求出对 x、y、z 三轴、OA 轴及 O点之矩。 答：Fx=Fcos，Fy=—Fsincos，Fz=Fsinsin； mx(F)= Fasin，my(F)=F(acoscos—rsin)， mz(F)=—F(acossin+rcos)； mOA(F)=—Fr； mO(F)= Fasini＋F(acoscos—rsin)j—F(acossinrcos)k 。 题1-6 图 题1-7 图 1-7 如图示在△ABC 平面内作用力偶（F，F），其中力 F 位于 BC 边上，F作用于 A点。已知 OA＝a，OB＝b，OC＝c，试求此力偶之力偶矩及其在三个坐标轴上的投影。 下列各题中假定物体接触处光滑。物体重量除图上标明外，均略去不计。 答：22222222),(;),(;),();(),(cbFabmcbFacmcbFbcmabacbccbFmzyxFFFFFFkjiFF。 1-8 画出下列各图中单个物体的受力图。 题1-8 图 1-9 画出下列各简单物系中指定物体的受力图。 题1 -9 图 1 -1 0 画出下列各复杂物系中指定物体的受力图。 题1-10 图 第2 章 力系的简化 2-1 三力作用在正方形上，各力的大小、方向及位置如图示，试求合力的大小、方向及位置。分别以 O 点和 A 点为简化中心，讨论选不同的简化中心对结果是否有影响。 答：45,N66.5N24xR，合力作用...