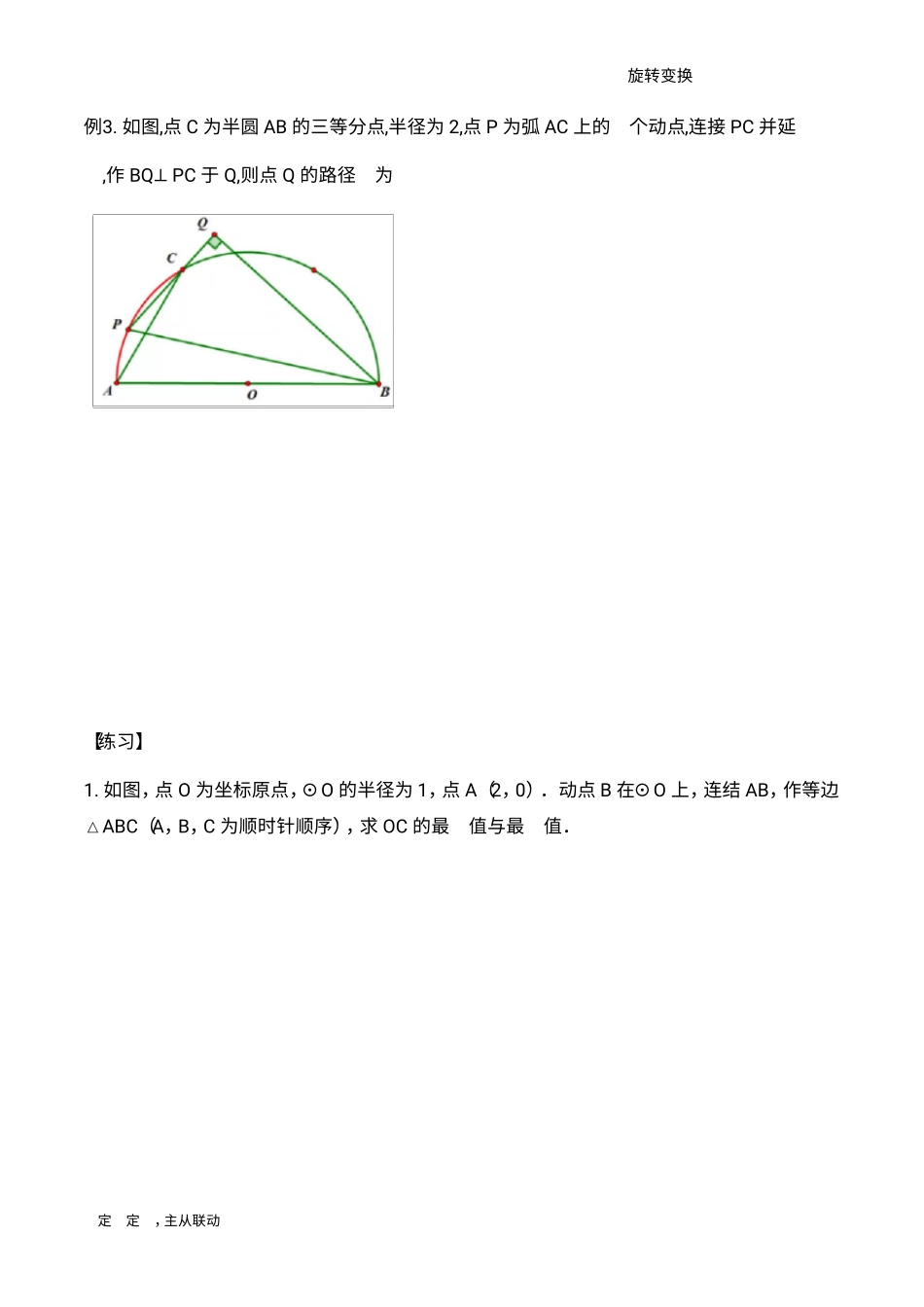
旋转变换定角定比,主从联动瓜豆原理——【曲线轨迹】例1. 如图所示,在平面直角坐标系中,已知点 A 的坐标为(2,3),P 点是以点 A 为圆心,半径为 2 的圆上的任意动点,(1)以 QP 为直角边作等腰直角三角形POQ,且 Q 点在第二象限内 ,求 AQ 的最小值及最大值(2)以 OQ 为斜边边作等腰直角三角形POQ,且 Q 点在第三象限内 ,求 AQ 的最小值及最大值旋转变换定角定比,主从联动例2. 如图,点 A 是双曲线 y=在第一象限上的动点,连接 AO 并延长交另一个分支于点 B,(1)以 AB 为斜边作等腰 Rt△ABC,点 C 在第二象限,随着点 A 的运动,点 C 的位置也不断变化,写出 C 点的轨迹在坐标系中所对函数的解析式(2)以 AB 为边作等边△ABC,C 在第三象限,写出C 点的轨迹在坐标系中所对函数的解析式(3)以 AB 为底边作等腰△ABC,∠C=120°在第三象限,写出C 点的轨迹在坐标系中所对函数的解析式旋转变换定角定比,主从联动例3. 如图,点 C 为半圆 AB 的三等分点,半径为 2,点 P 为弧 AC 上的一个动点,连接 PC 并延长,作 BQ⊥ PC 于 Q,则点 Q 的路径长为【练习】1. 如图,点 O 为坐标原点,⊙ O 的半径为 1,点 A(2,0).动点 B 在⊙ O 上,连结 AB,作等边△ ABC(A,B,C 为顺时针顺序),求 OC 的最大值与最小值.旋转变换定角定比,主从联动2. 如图,点 C 是半圆上一动点,以 AC 为边向下作正方形 ACDE,连 OE,若 AB=4m ,则 OE 的最大值为3. 如图,AB=4,O 为 AB 的中点,⊙ O 的半径为 1.点 P 是⊙ O 上一动点,以 PB 为直角边的等腰直角 △ PBC(点 P,B,C 按逆时针方向排列) ,则线段 AC 长的取值范围是 _____________.旋转变换定角定比,主从联动4. 如图,AB 为⊙ O 的直径,点 C 在 AB 的延长线上,AB=6,BC=3,P 是⊙ O 上的一个动点,连接 CP,以 CP 为底边在 PC 的上方作等腰三角形 PCD,且使∠ DCP=30°,连接 OD,OD 长的最小值为5. 如图,AB 是⊙ 的直径,点 C 在 AB 的延长线上,AB=BC=10,P 是⊙ O 上一动点,连接 PC,以 PC 为边作△ PCD,使∠ PDC=90°,tan∠ DPC=,P,C,D 三点为逆时针顺序.连接 OD,则线段 OD 长的最小值是________.旋转变换定角定比,主从联动6. 如图,点 O 在线段 AB 上,OA=1,OB=2.以点 O 为圆心,OA 长为半径的圆为 ⊙ O.在⊙ O上取动点 P,以 P...