第一章4卢瑟福散射公式

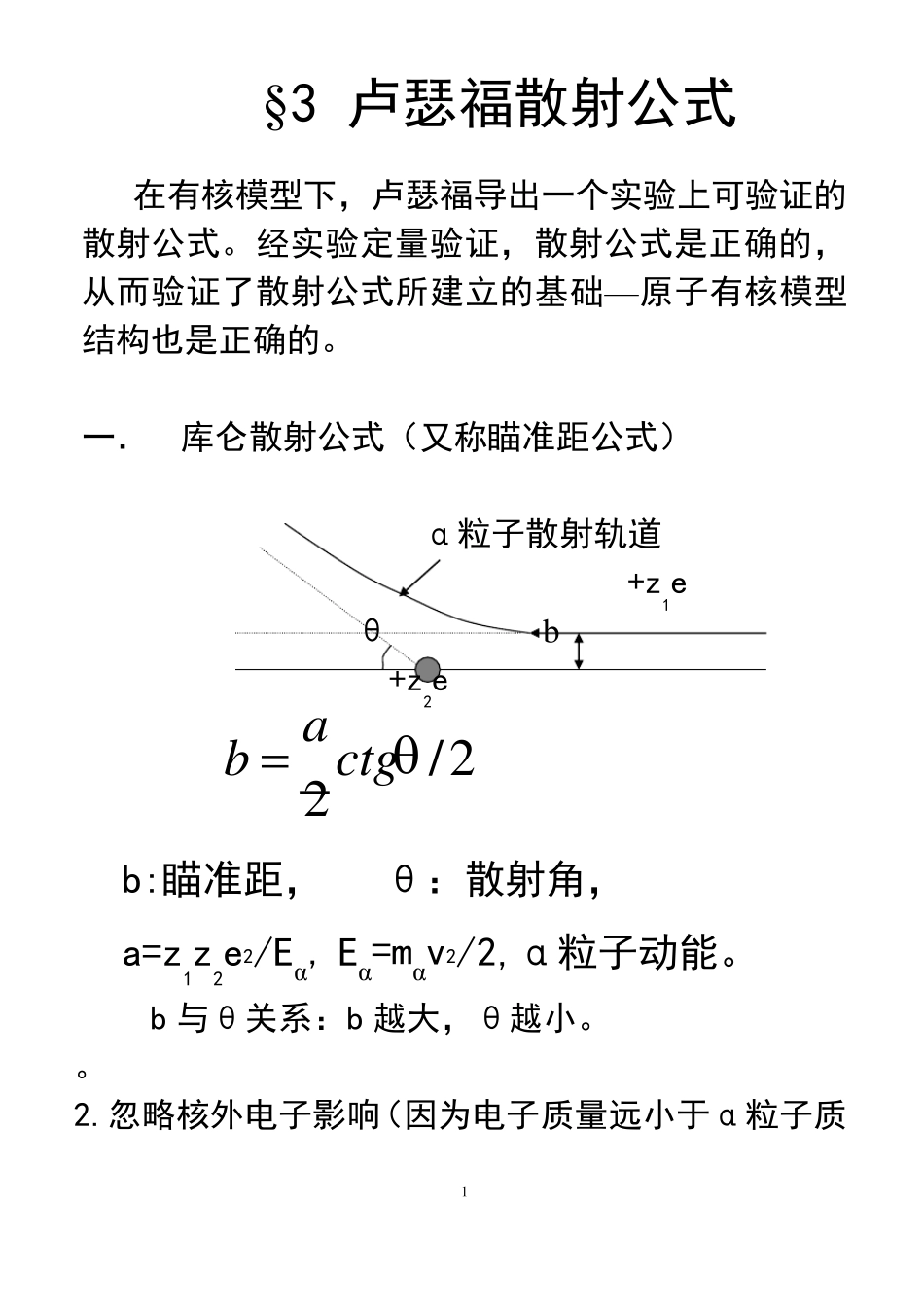
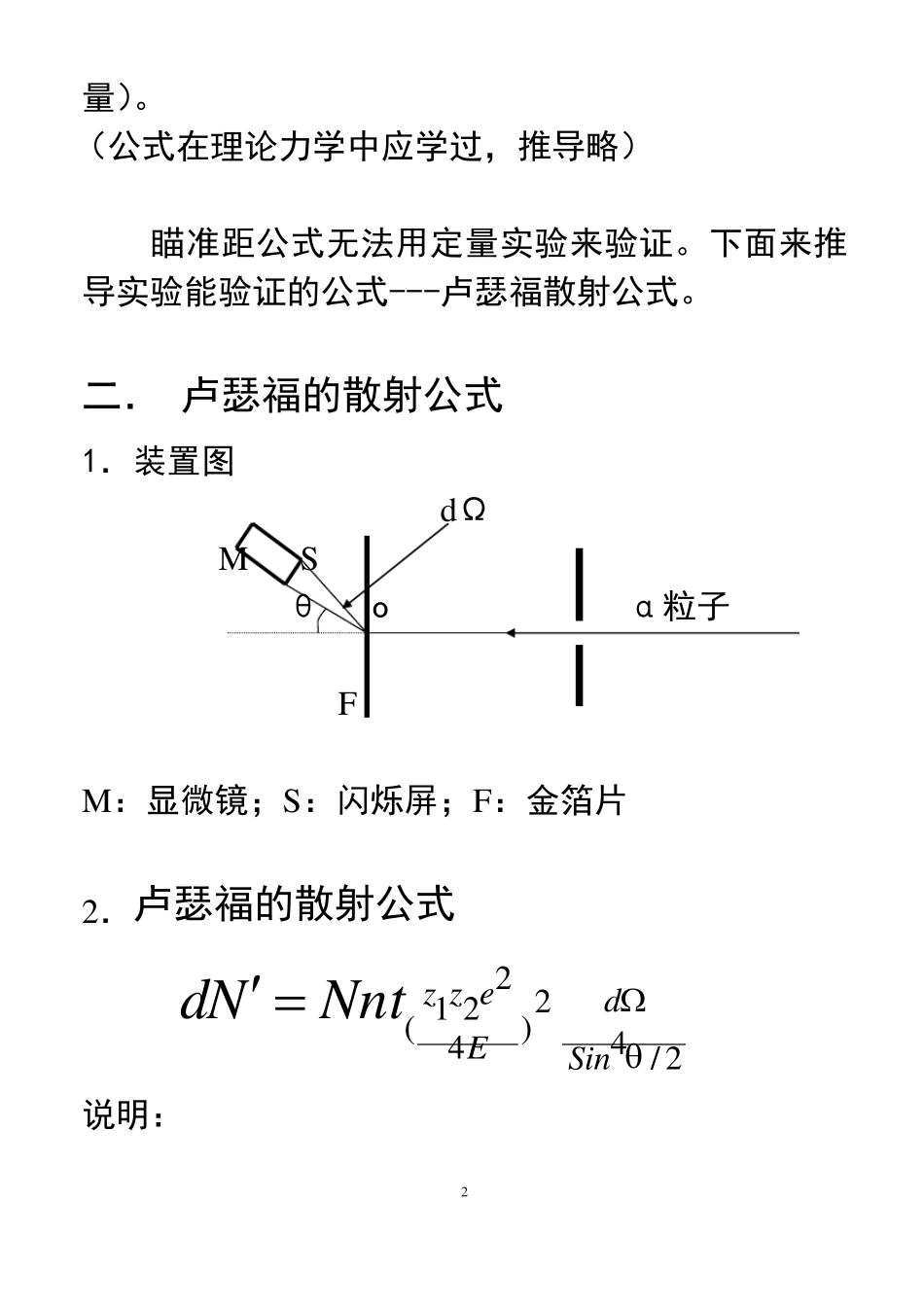
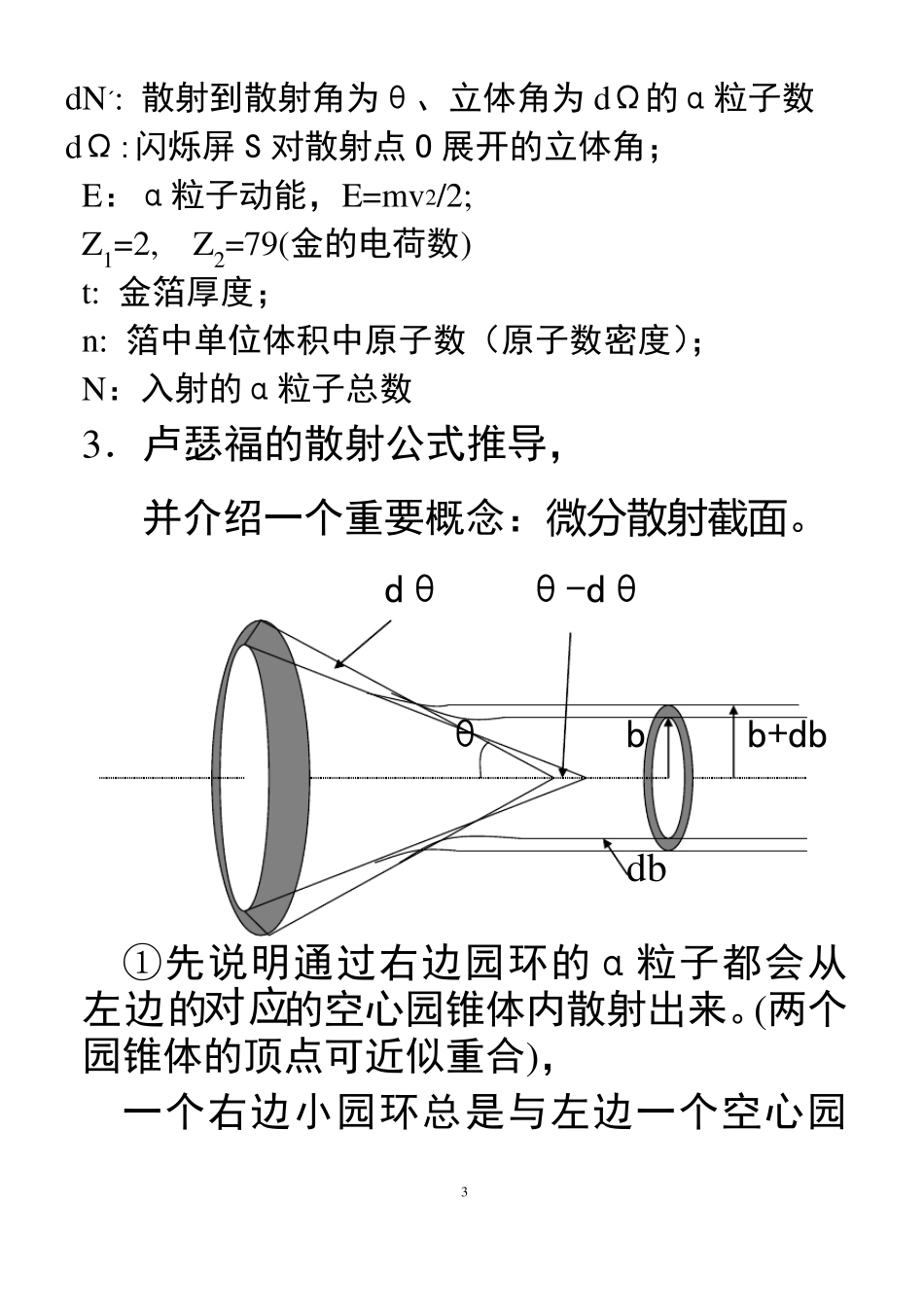
1 § 3 卢瑟福散射公式 在有核模型下，卢瑟福导出一个实验上可验证的散射公式。经实验定量验证，散射公式是正确的，从而验证了散射公式所建立的基础—原子有核模型结构也是正确的。 一． 库仑散射公式（又称瞄准距公式） α粒子散射轨道 +z1e θ b +z2e 2/2ctgab  b:瞄准距， θ：散射角， a=z1z2e2/Eα, Eα=mαv2/2,α粒子动能。 b 与θ关系：b 越大，θ越小。 。 2.忽略核外电子影响（因为电子质量远小于α粒子质 2 量）。 （公式在理论力学中应学过，推导略） 瞄准距公式无法用定量实验来验证。下面来推导实验能验证的公式---卢瑟福散射公式。 二． 卢瑟福的散射公式 1．装置图 dΩ M S θ o α粒子 F M：显微镜；S：闪烁屏；F：金箔片 2．卢瑟福的散射公式 2/42)4221(SindEezzNntNd 说明： 3 dN´: 散射到散射角为θ、立体角为dΩ的α粒子数 dΩ:闪烁屏 S 对散射点 O 展开的立体角； E：α粒子动能，E=mv 2/2; Z1=2, Z2=79(金的电荷数) t: 金箔厚度； n: 箔中单位体积中原子数（原子数密度）； N：入射的α粒子总数 3．卢瑟福的散射公式推导， 并介绍一个重要概念：微 分散射截面。 dθ θ-dθ θ b b+db db ①先说明通过右边园环的α粒子都会从左边的对应的空心园锥体内散射出来。(两个园锥体的顶点可近似重合)， 一个右边小园环总是与左边一个空心园 4 锥体对应。 现推导小园环d σ与空心园锥体的立体角d Ω的关系： dCosSinrrSinrdrdSd22422221 62822222222242322SindaSindCosaSindactgadbbd 这就是 d Ω与dσ的关系式。并且由于对称性，此式对出射的任意立体角 d Ω'与对应的入射小截面 dσ'的关系也成立。 ②求与一个原子核碰撞，从 d Ω散射出来的α粒子数 dN(假设 α 粒子穿过箔片时只发生 5 一次散射) 面积A 入射α 粒子 散射α 粒子 厚度t 设通过A 的入射α粒子总数为 N，则单位面积上通过α 粒子数为 N/A，那么通过某一小截面dσ 的α 粒子数为： dSinANadANdN21642 这是 α 粒子与一个原子核碰撞，散射到散射角为 θ、立体角为 dΩ 的α 粒子数 dN。 ③ 那么被 A 面积中所有原子核散射到散射到同一散射角为 θ、立体角为 dΩ 的α 粒子数 dN'为： 6 dSinEezzntNNddSinantNntNdAntdNNd21)4...