第一章集合与常用逻辑用语知识结构

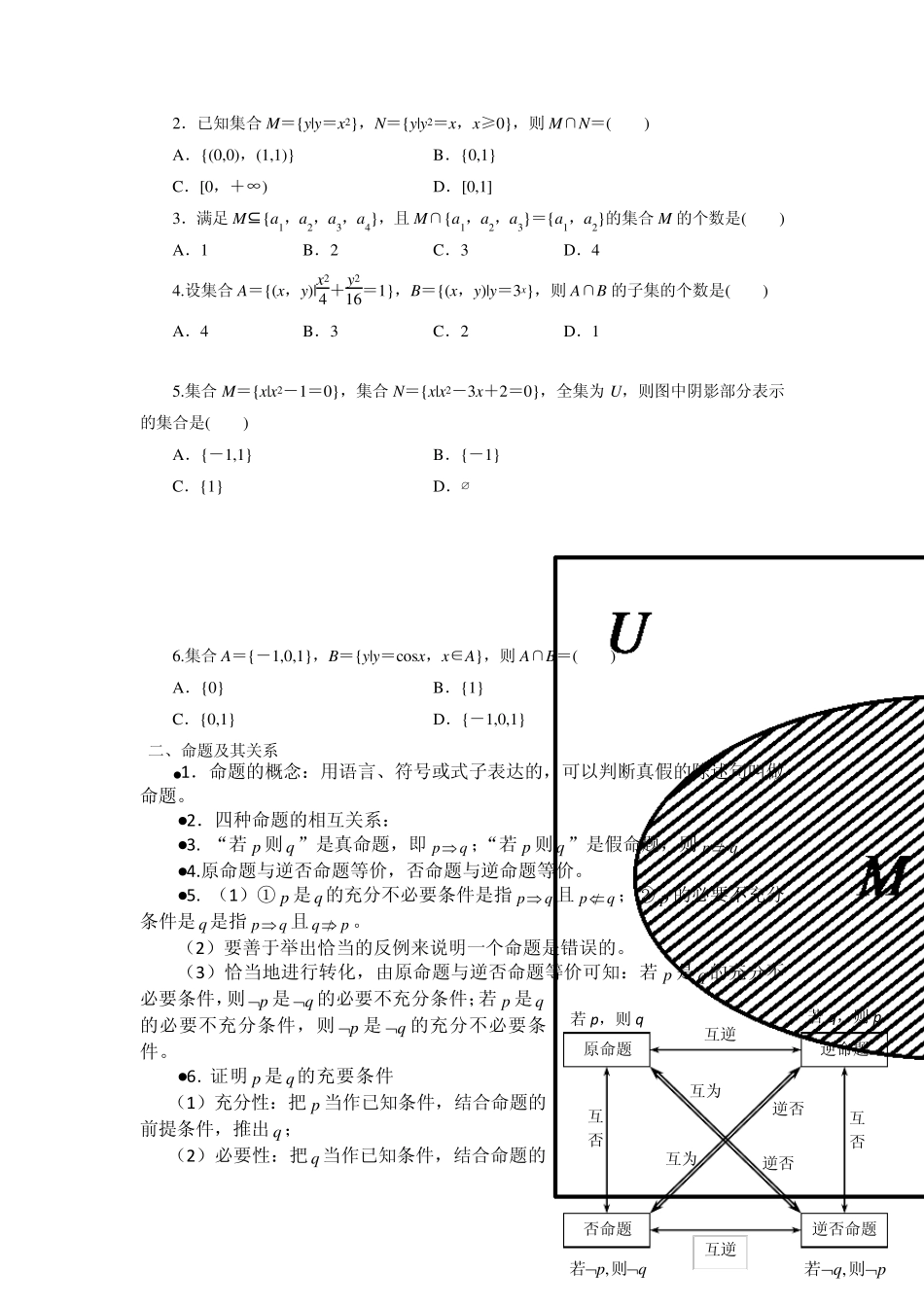
第一章 集合与常用逻辑用语知识结构 【知识概要】 一、集合的概念、关系与运算 ●1. 集合中元素的特性：确定性、互异性、无序性. ●2. 集合的表示方法：列举法、描述法. 图示法表示，常用的集合符号，如,,,,,,N NNZ R Q  ●3. 元素与集合的关系：我们把研究对象统称为元素，把一些元素组成的总体叫做集合，若元素x是集合A 的元素，则x A ，否则x A 。 ●4. 集合与集合之间的关系： ①子集：若x A ，则x B ，此时称集合A 是集合B 的子集，记作AB。 ②真子集：若AB，且存在元素x B ，且x A ，则称A 是B 的真子集，记作：A B. ③相等：若AB，且AB，则称集合A 与B 相等，记作A＝B.。 ●5. 集合的基本运算： ①交集：A Bx x Ax BI且 ②并集：{}A Bx x Ax BU或 ③补集：{ |,}UC Ax x Ux A且，其中U 为全集，AU。 ●6. 集合运算中常用结论： ① ,,AAAAA BBA IIII，ABAABI。 ② ,,AAAAAA BBAUUUU ，A BABAU。 ③()UAC AUU，()UC AA I， ()()(UUUCABCACBIU，() () ()UUUCA BC AC BUI。 ④由n个元素所组成的集合，其子集个数为2n 个。真子集个数为2n -1，非空真子集个数为2n -2 ⑤空集是任何集合的子集，即A 一、选择题 1.已知全集U＝{1,2,3,4,5,6,7,8} ，M＝{1,3,5,7} ，N＝{5,6,7} ，则∁U(M∪N)＝( ) A．{5,7} B．{2,4} C．{2,4,8} D．{1,3,5,6,7}   2．已知集合M＝{y|y＝x2} ，N＝{y|y2＝x，x≥0} ，则M∩N＝( ) A．{(0,0)，(1,1)} B．{0,1} C．[0，＋∞) D．[0,1] 3．满足M⊆{a1，a2，a3，a4} ，且M∩{a1，a2，a3} ＝{a1，a2} 的集合M 的个数是( ) A．1 B．2 C．3 D．4 4.设集合A＝{(x，y)|x24＋y216＝1} ，B＝{(x，y)|y＝3x} ，则A∩B 的子集的个数是( ) A．4 B．3 C．2 D．1 5.集合M＝{x|x2－1＝0} ，集合N＝{x|x2－3x＋2＝0} ，全集为U，则图中阴影部分表示的集合是( ) A．{－1,1} B．{－1} C．{1} D．∅ 6.集合A＝{－1,0,1} ，B＝{y|y＝cosx，x∈A} ，则A∩B＝( ) A．{0} B．{1} C．{0,1} D．{－1,0,1} 二、命题及其关系 ●1．命题的概念：用语言、符号或式子表达的，可以判断真假的陈述句叫做命题。 ●2．四种命题的相互关系： ●3. “若 p 则q”是真命题，即 pq ；“若 p 则q”...