第二章材料的断裂强度

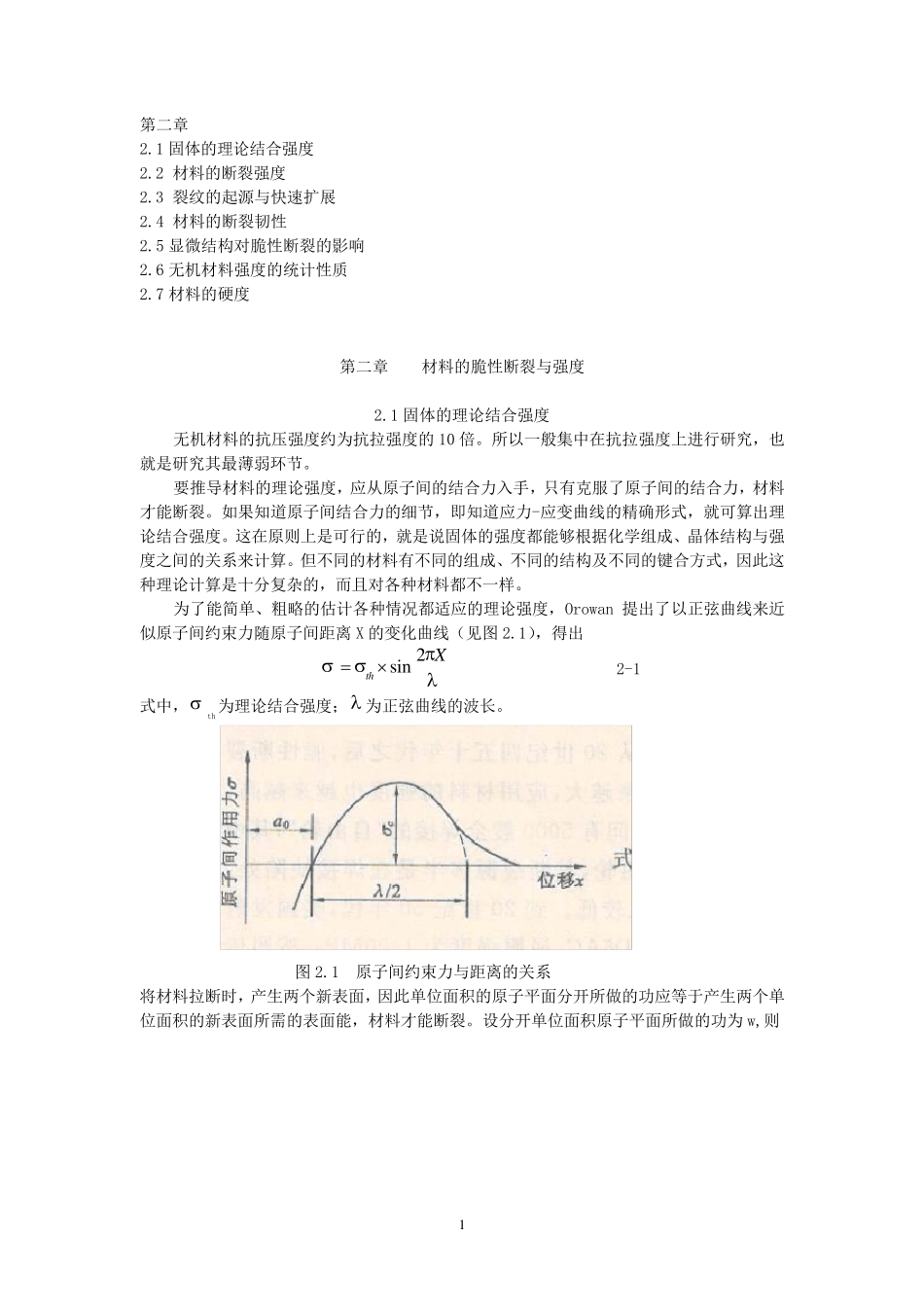
1 第二章 2.1 固体的理论结合强度 2.2 材料的断裂强度 2.3 裂纹的起源与快速扩展 2.4 材料的断裂韧性 2.5 显微结构对脆性断裂的影响 2.6 无机材料强度的统计性质 2.7 材料的硬度 第二章 材料的脆性断裂与强度 2.1 固体的理论结合强度 无机材料的抗压强度约为抗拉强度的10 倍。所以一般集中在抗拉强度上进行研究，也就是研究其最薄弱环节。 要推导材料的理论强度，应从原子间的结合力入手，只有克服了原子间的结合力，材料才能断裂。如果知道原子间结合力的细节，即知道应力-应变曲线的精确形式，就可算出理论结合强度。这在原则上是可行的，就是说固体的强度都能够根据化学组成、晶体结构与强度之间的关系来计算。但不同的材料有不同的组成、不同的结构及不同的键合方式，因此这种理论计算是十分复杂的，而且对各种材料都不一样。 为了能简单、粗略的估计各种情况都适应的理论强度，Orowan 提出了以正弦曲线来近似原子间约束力随原子间距离X 的变化曲线（见图2.1），得出 Xth2sin 2-1 式中，th为理论结合强度； 为正弦曲线的波长 。 图2.1 原子间约束力与距离的关系 将 材料拉断时 ，产 生 两 个 新 表 面 ，因此单位 面 积 的原子平 面 分开 所做 的功 应等 于 产 生 两 个 单位 面 积 的新 表 面 所需 的表 面 能，材料才能断裂。设 分开 单位 面 积 原子平 面 所做 的功 为w,则 2 thththxdxxw]2cos[202022sin 2-2 设 材 料 形 成 新 表 面 的 表 面 能 为  （ 这 里 是 断 裂 表 面 能 ， 不 是 自 由 表 面 能 ）， 则 w=2 ,即 2th ,2th 2-3 接 近 平 衡 位 置 o 的 区 域 ， 曲 线 可 以 用 直 线 代 替 ， 服 从 虎 克 定 律 : EaxE 2-4 a 为 原 子 间 距 。 X 很 小 时 sinxx22 2-5 将 （ 2.3），（ 2.4） 和 （ 2.5） 式 代 入 （ 2.1） 式 ， 得 aEth 2-6 式 中 a 为 晶 格 常 数 ， 随 材 料 而 异 。 可 见 理 论 结 合 强 度 只 与 弹 性 模 量 、 表 面 能 和 晶 格 距 离 等 材料 常 数 有 关 ， 属 于 材 料 的 本 证 性 能 。（ 2.6） 式 虽 然 是 粗 略 的 估 计 ...