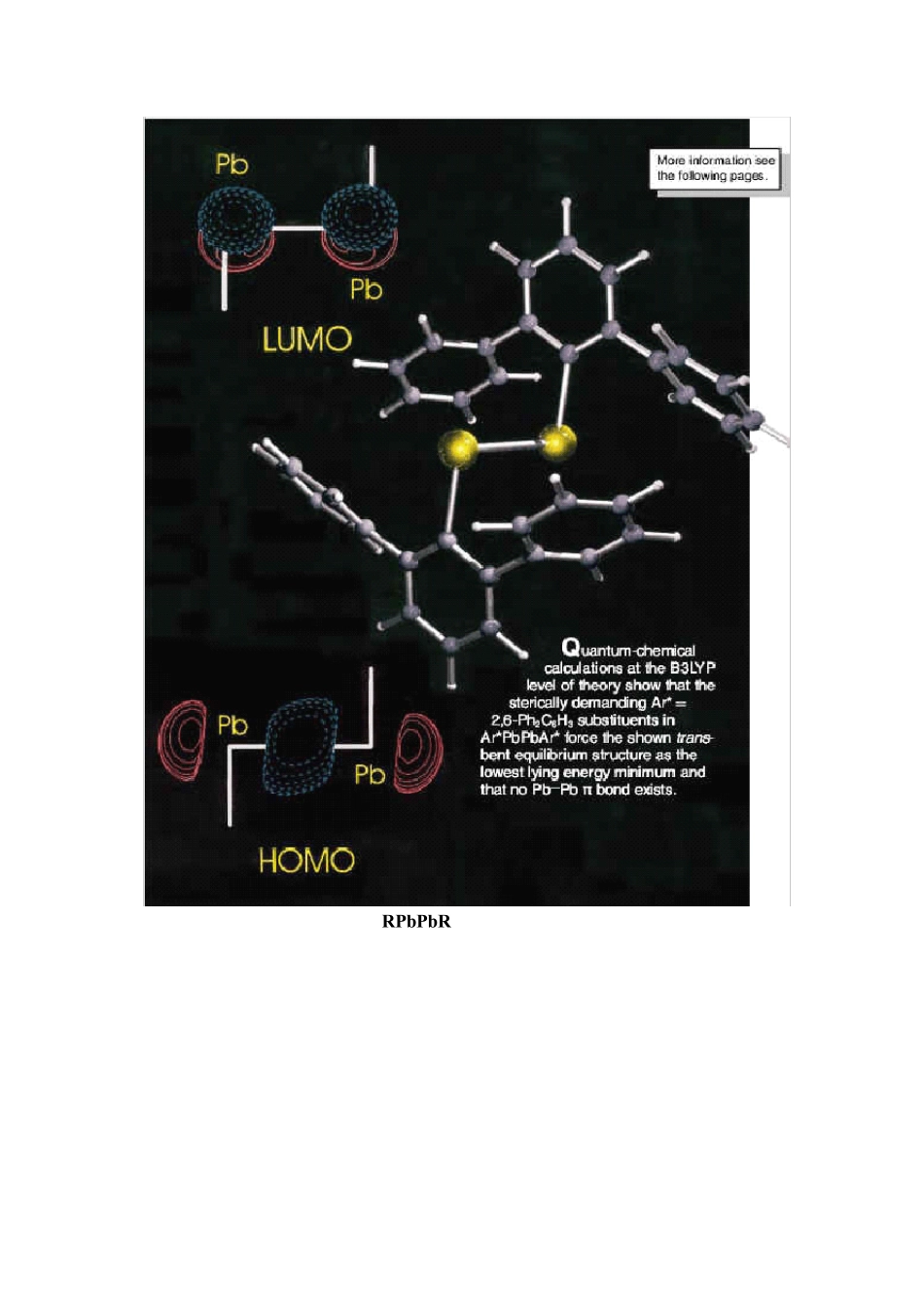
4 .群表示的理论基础和分子对称性教学目标与学习指导1.本章第1节讨论分子对称性。要求掌握五种对称元素和对称操作的乘积的概念。2.本章第2节介绍群的基本知识。要求对群的基本知识有一般的了解。3.本章第3节讨论分子点群。要求掌握分子点群的确定。4 .本章第4 节讨论分子对称操作的矩阵表示。要求掌握五种对称操作的矩阵表示法。5.本章第5节讨论群表示的基及群的表示。要求对群表示的一般性质有所了解。要求掌握不可约表示和可约表示的概念以及可约表示的约化,了解特征标表。4 -1分子对称性4 -2群的基本知识4 -3分子对称操作群4 -4 分子对称操作的矩阵表示(选修)4 -5群表示的基及群的表示(选修)群论是从实践中发展起来的一门比较抽象的数学。但把它的基本理论与物质结构的具体对称性相结合之后,群论就成为研究物质微粒运动规律的一种有力工具。在有关基本粒子、核结构、原子结构、分子结RPbPbR 的键合性质YuChen,MichaelHartmann,MichaelDiedenhofen,andGernotFrenking*Angew.Chem.Int.Ed.2001,40,No.11,2052构以及晶体结构等问题的理论研究和计算中经常用到群论方法。由于自然学科彼此间的交叉、渗透,在近代化学领域内,研究化学键理论和分子动力学,应用各种波谱技术等方面,群论已成为重要的工具。4-1分子对称性对称性是物体所具有的,实施对称操作之前后不可分辨的性质。通过研究分子的对称性,一方面可以把握分子结构的特点及说明分子的有关性质;另一方面,也可借助于分子对称性,使求解薛定谔方程的过程大为简化。原子轨道、分子轨道及分子的几何构型的对称性,是电子运动状态及分子结构特点的内在反映。4-1-1对称操作与对称元素4-1-2对称操作的乘积4-1-1对称操作与对称元素对称操作:每一次操作都能够产生一个与原来图形等价的图形。也就是,当一个操作作用于一个分子上,所产生的新分子几何图形和作用前的图形如不借助于标号是无法区分的。对称元素:对分子几何图形施行对称操作时,所依赖的几何要素(点、线、面及其组合)称为对称元素。(1)恒等操作与恒等元素恒等操作后,分子保持完全不动。用符号 E表示。例如,将一个分子旋转360度相应于分子没有转动。(2)旋转与旋转轴只能找到1根旋转轴的对称类型叫单轴群,用符号 Cn表示。对称轴(Cn)对应与旋转操作(Cn,Cn2,Cn3…..Cnn-1,Cnn=E)在 Cn操作中,绕分子对称轴施行旋转θ角度,则 n=360°/θ。例如,对下面正三角形,分步施行绕垂直于三角形平面的旋转对称轴...