25有限元法在流体力学中的应用

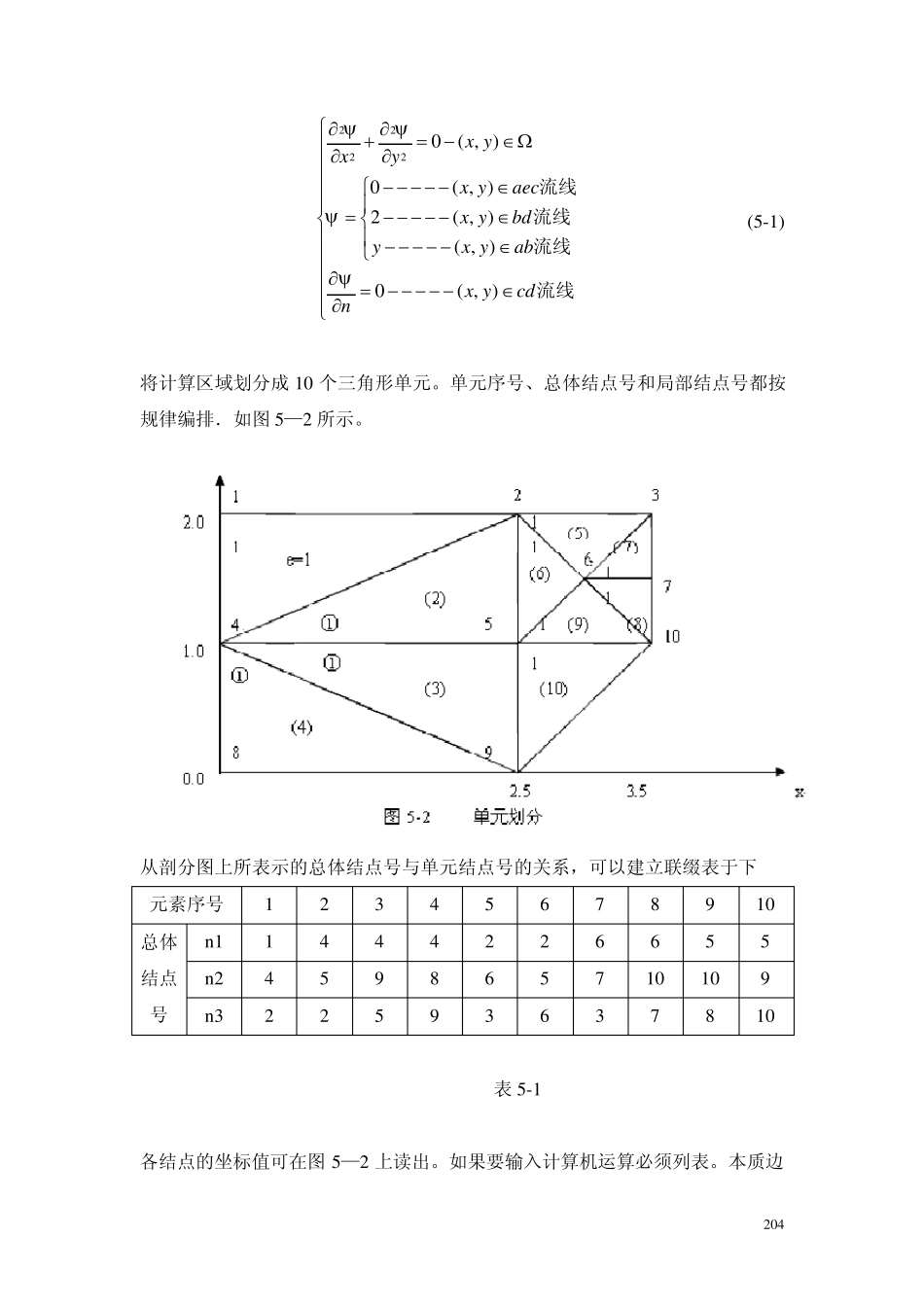
203 第五章 有限元法在流体力学中的应用 本章介绍有限元法在求解理想流体在粘性流体运动中的应用。讨论了绕圆柱体、翼型和轴对称物体的势流，分析了求解粘性流动的流函数—涡度法流函数法和速度—压力法，同时导出粘性不可压流体的虚功原理。 §1 不可压无粘流动 真实流体是有粘性和可压缩的，理想不可压流体模型使数学问题简化，又能较好地反映许多流动现象。 1. 圆柱绕流 本节详细讨论有限无法的解题步骤。考虑两平板间的圆柱绕流．如图 5—1 所示。为了减小计算工作量，根据流动的对称性可取左上方的l／4 流动区域作为计算区域。 选用流函数方法，则流函数 应满足以下 Lap lace 方程和边界条件 2 0 4 22220( , )0( , )2( , )( , )0( , )x yxyx yaecx ybdyx yabx ycdn                   流线流线流线流线 (5 -1 ) 将计算区域划分成1 0 个三角形单元。单元序号、总体结点号和局部结点号都按规律编排．如图5 —2 所示。 从剖分图上所表示的总体结点号与单元结点号的关系，可以建立联缀表于下 元素序号 1 2 3 4 5 6 7 8 9 1 0 总体结点 号 n 1 1 4 4 4 2 2 6 6 5 5 n 2 4 5 9 8 6 5 7 1 0 1 0 9 n 3 2 2 5 9 3 6 3 7 8 1 0 表 5 -1 各结点的坐标值可在图5 —2 上读出。如果要输入计算机运算必须列表。本质边 205 界结点号与该点的流函数值列于下表 边界结点号n 1 2 3 4 8 9 10 流函数Φ 2 2 2 1 0 0 0 表5-2 选用平面线性三角形元素，插值函数为(3—15)式。对二维 Lap lace 方程进行元素分析，得到了单元系数矩阵计算公式(3—19)和输入向量计算公式(3—20)。现在对全部元素逐个计算系数矩阵。 例如元素1，其结点坐标为1x =0, 1y =2; 2x =0, 2y =1; 3x =2.5, 3y =2. 由(3—15)式可得 1322.5axx; 2132.5axx  3210axx, 1231byy  ; 2310byy; 3121byy; 01.25A  从(3—19)式可计算出1K 11.451.250.21.2500.2K 对称 依次可计算出全部子矩阵 20.20.201.451.251.25K  30.200.21.251.251.45K  206 4...