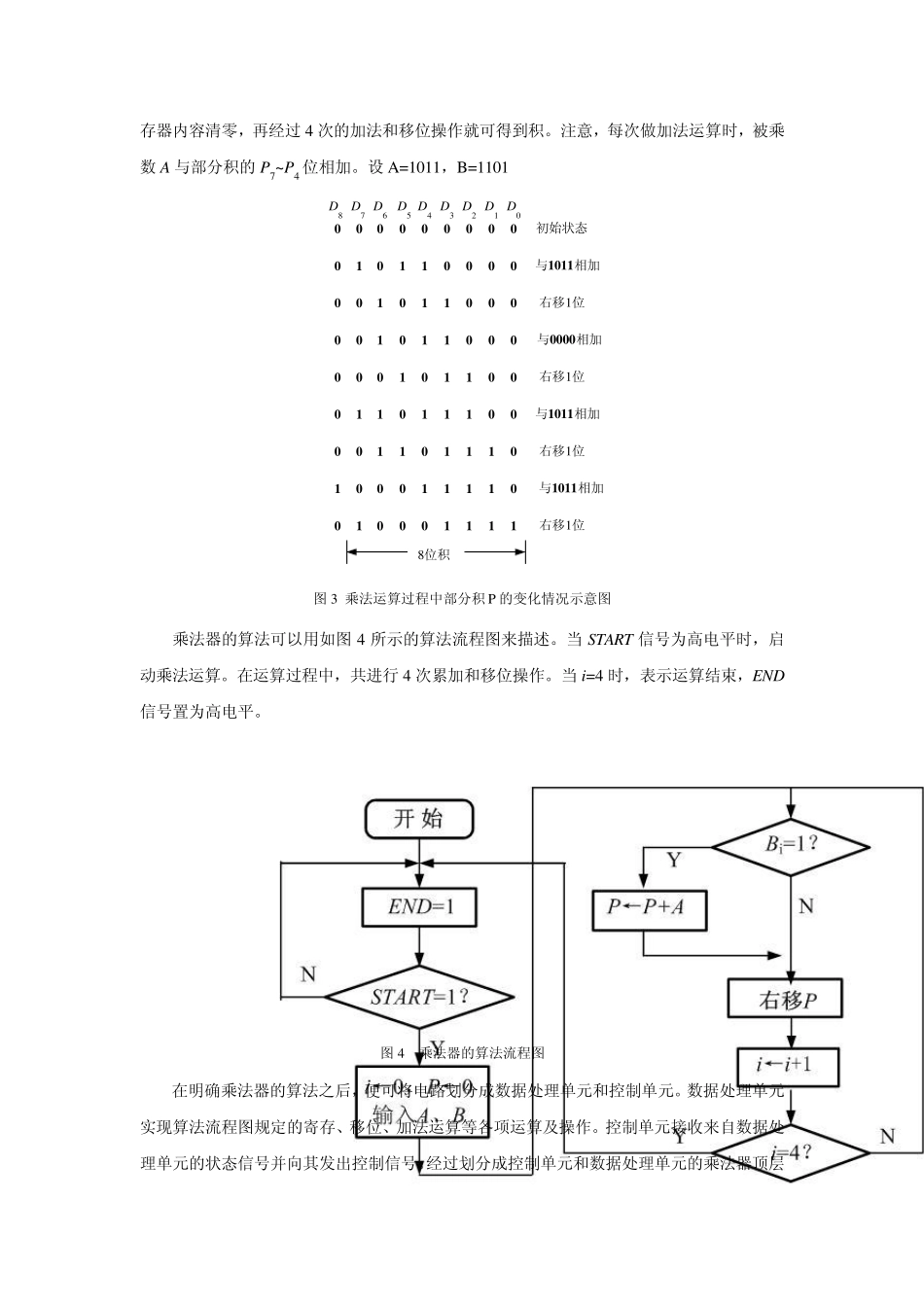
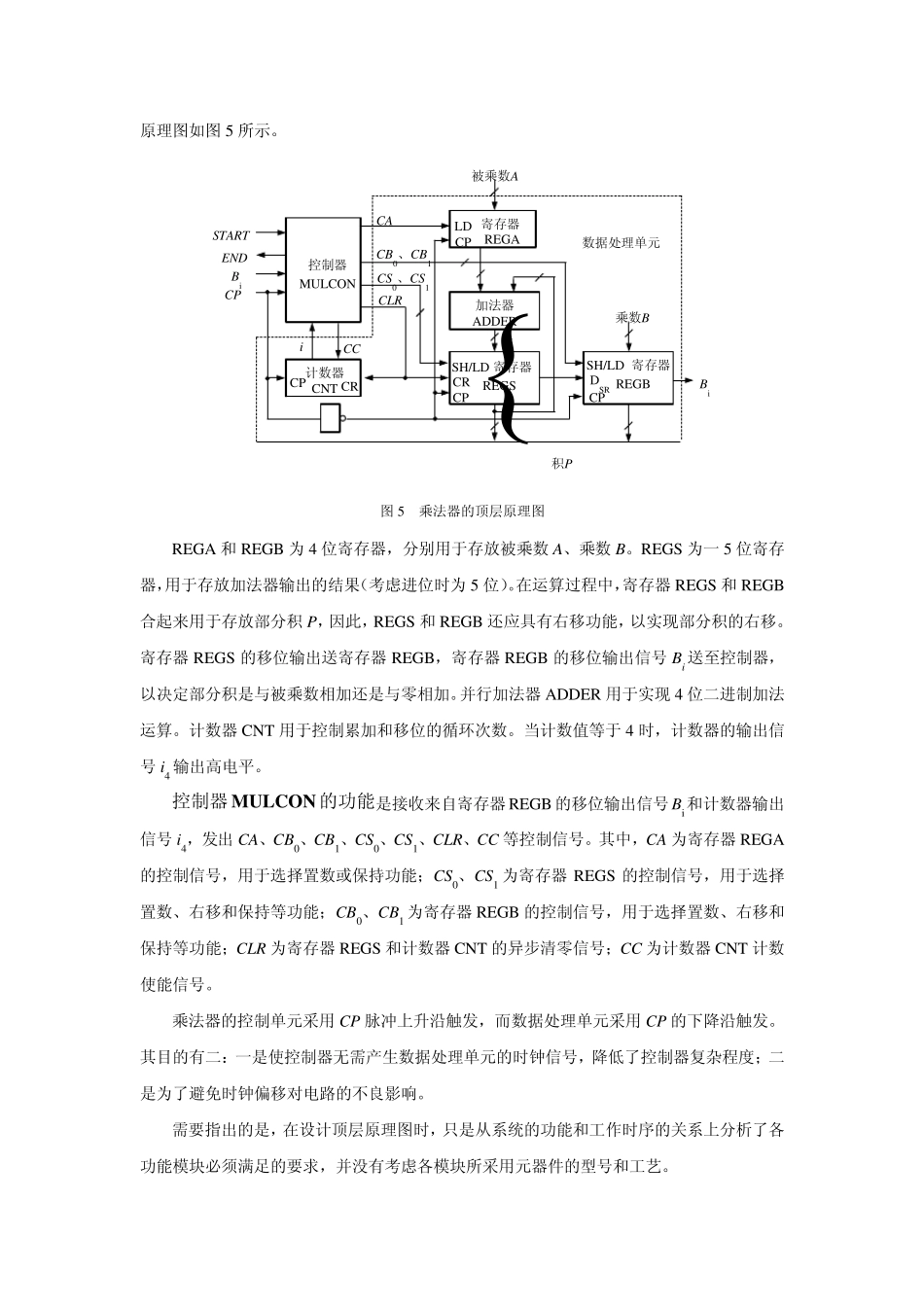
4*4 数字乘法器设计 1 .设计任务 试设计一4 位二进制乘法器。4 位二进制乘法器的顶层符号图如图1 所示。 MULENDP844ABSTART1 0 1 11 1 0 1×1 0 1 10 0 0 01 0 1 11 0 1 11101 1001 图1 4 位乘法器顶层符号图 图2 4 位乘法运算过程 输入信号:4 位被乘数 A(A3 A2 A1 A0),4 位乘数 B(B3 B2 B1 B0),启动信号START。 输出信号:8 位乘积 P(P7 P6 P5 P4 P3 P2 P1 P0),结束信号END。 当发出一个高电平的START 信号以后,乘法器开始乘法运算,运算完成以后发出高电平的END 信号。 2 .顶层原理图设计 从乘法器的顶层符号图可知,这是一个 9 输入 9 输出的逻辑电路。一种设计思想是把设计对象看作一个不可分割的整体,采用数字电路常规的设计方法进行设计,先列出真值表,然后写出逻辑表达式,最后画出逻辑图。这种设计方法有很多局限性,比如,当设计对象的输入变量非常多时,将不适合用真值表来描述,同时,电路功能任何一点微小的改变或改进,都必须重新开始设计。另一种设计思想是把待设计对象在逻辑上看成由许多子操作和子运算组成,在结构上看成有许多模块或功能块构成。这种设计思想在数字系统的设计中得到了广泛的应用。 对于 4 位乘法器而言,设A=1 0 1 1 ,B=1 1 0 1 ,则运算过程可由图2 所示。从乘法运算过程可知,乘法运算可分解为移位和相加两种子运算,而且是多次相加运算,所以是一个累加的过程。实现这一累加过程的方法是,把每次相加的结果用部分积 P 表示,若 B 中某一位 Bi=1 ,把部分积 P 与 A 相加后右移 1 位;若 B 中某一位Bi= 0 ,则部分积 P 与 0 相加后右移1 位(相当于只移位不累加)。通过 4 次累加和移位,最后得到的部分积 P 就是 A 与 B 的乘积。 为了便于理解乘法器的算法,将乘法运算过程中部分积 P 的变化情况用图3 表示出来。存放部分积的是一个 9 位的寄存器,其最高位用于存放在做加法运算时的进位输出。先把寄存器内容清零,再经过4 次的加法和移位操作就可得到积。注意,每次做加法运算时,被乘数A 与部分积的P7~P4 位相加。设A=1011,B=1101 000000000初始状态010110000与1011相加001011000右移1位001011000与0000相加000101100右移1位011011100与1011相加001101110右移1位100011110与1011相加010001111右移1位D0D1D2D3D4D5D6D7D88位积 图3 乘法运算过程中部分积P 的变化情...