5.运筹学之运输问题(胡运权版)

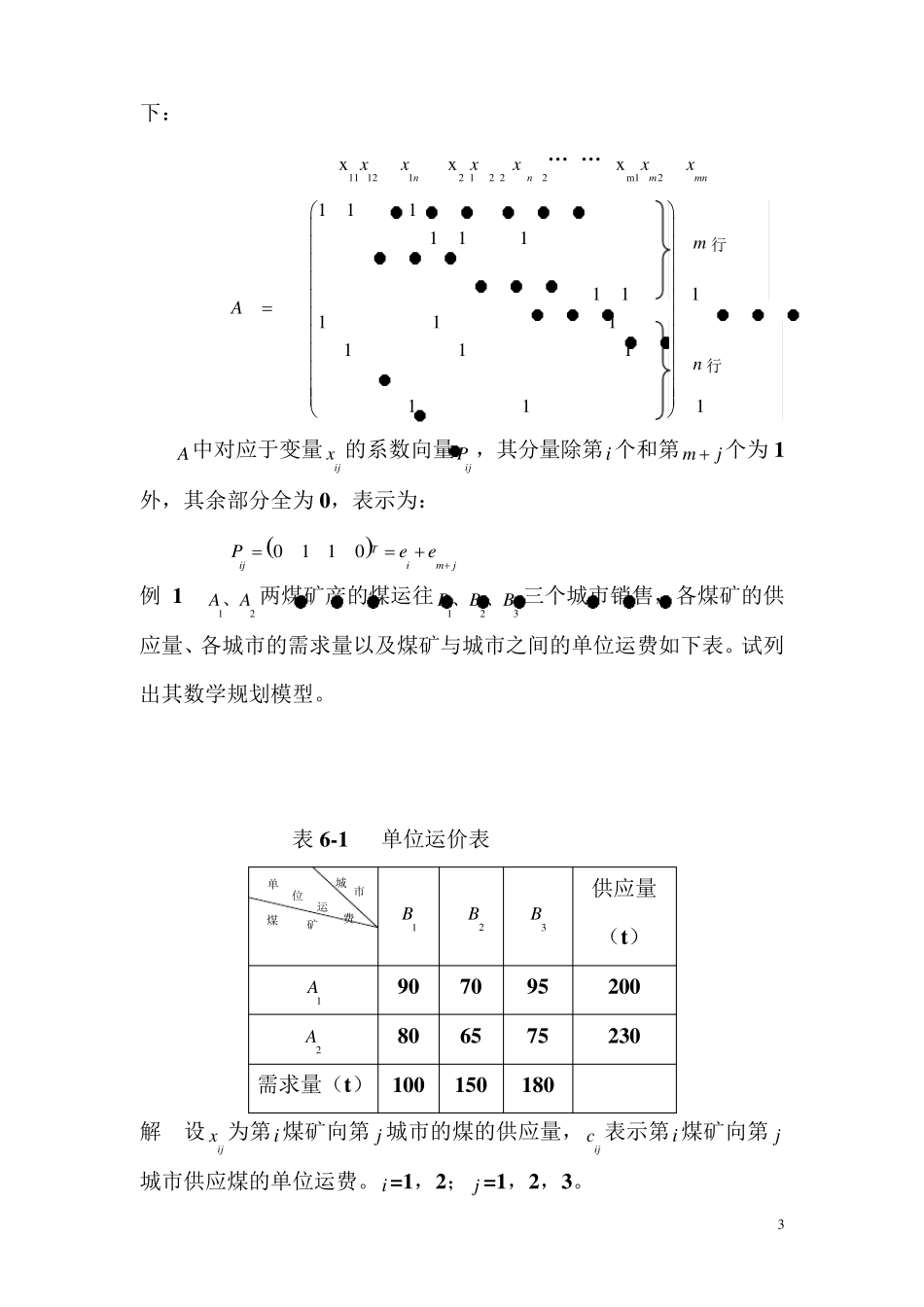
1 第六章 运输问题 运输问题依然属于线性规划问题的范畴，但是由于其约束方程组的系数矩阵具有特殊的结构，因而可以找到一种比单纯形表更简便的求解方法，正是基于此，运输问题从线性规划中单列出来进行讨论。本章分为两大部分，前三节介绍求运输问题单纯形方法——表上作业法，第四节重点介绍运用EXCEL电子表格模型解决运输问题。 §1 运输问题的模型与性质 1.1 运输问题模型 运输问题的一般提法是这样的：某种物资有若干个产地和销地，若已知各个产地的产量、各个销地的销量以及各产地到各销地的单位运价（或运输距离）。问应如何组织调运，才能使总运费（或总的运输量）最省？ 将此问题更具体化，假定有m 个产地，n 个销地， ia ——第i产地的供应量，i=1，2，…，m 。 jb ——第j 销地的需求量，j =1，2，…，n 。 ijc ——从产地i到销地 j 的单位运费，i =1，2，…，m ，j =1，2，…，n 。 ijx ——产地i到销地 j 的调运数量。 则该问题为求解最佳调运方案，即求解所有ijx 的值，使总的运输 2 费用 11mnijijijc x达到最少。决策变量为ijx 。 该问题的数学模型形式为： minz 11mnijijijc x . .st 1mijixjb ， j =1，2，…，n 。 1 nijjx ia ， i=1，2，…，m 。 ijx 0 ，对所有的i，j 。 根据该问题中总需求量1miia与总供应量1njjb的关系，可将运输问题分为两类： 1、当1miia = 1njjb时，为平衡型运输问题； 2、当1miia ≠ 1njjb 时，为不平衡型运输问题。 实际上不平衡型运输问题可以转换为平衡型运输问题，我们首先讨论平衡型运输问题，在§3中介绍不平衡型向平衡型的转换。 平衡型运输问题的数学模型形式可表示为： minz 11mnijijijc x . .st 1mijix = jb ， j =1，2，…，n 。 1 nijjx = ia ， i=1，2，…，m 。 ijx 0 ，对所有的i，j 该模型包含有mn 个变量，mn 个约束方程，其系数矩阵 A 如 3 下： 11 121xnxx 2 12 22xnxx … … m12xmmnxx A 111 111 11 11 1 1 1 1 1 1 1 1 A中对应于变量ijx 的系数向量ijP ，其分量除第i个和第 mj 个为 1外，其余部分全为 0，表示为： 0110 TijimjPee 例 1 12AA、两煤矿产的煤运往123BBB、、三个城市销...