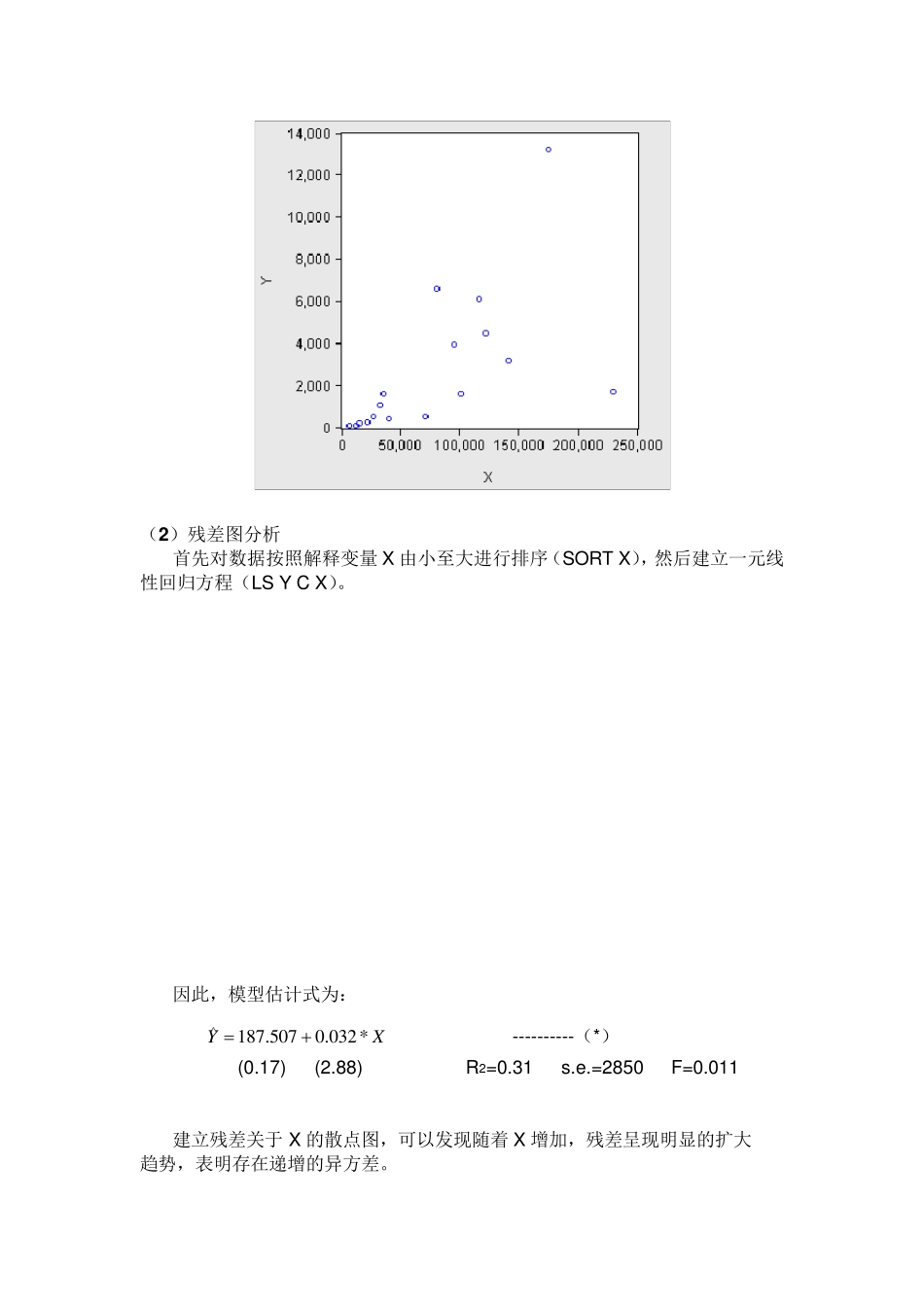
实验一 异方差性 【实验目的】 掌握异方差性问题出现的来源、后果、检验及修正的原理,以及相关的Eview s 操作方法。 【实验内容】 以《计量经济学学习指南与练习》补充习题4-16 为数据,练习检查和克服模型的异方差的操作方法。 【4-16】表 4-1 给出了美国 18 个行业 1988 年研究开发(R&D)费用支出Y 与销售收入 X 的数据。请用帕克(Park)检验、戈里瑟(Gleiser)检验、G-Q 检验与怀特(White)检验来检验Y 关于 X 的回归模型是否存在异方差性?若存在异方差性,请尝试消除它。 表 4-1 单位:百万美元 序号 研究开发费用 Y 销售收入 X 1 62.5 6375.3 2 92.9 11626.4 3 178.3 14655.1 4 258.4 21869.2 5 494.7 26408.3 6 1083.0 32405.6 7 1620.6 35107.7 8 421.7 40295.4 9 509.2 70761.6 10 6620.1 80522.8 11 3918.6 95294.0 12 1595.3 101314.1 13 6107.5 116141.3 14 4454.1 122315.7 15 3163.8 141649.9 16 13210.7 175025.8 17 1703.8 230614.5 【实验步骤】 一 检查模型是否存在异方差性 1 、图形分析检验 (1 )散点相关图分析 做出销售收入 X 与研究开发费用 Y 的散点相关图(SCAT X Y)。观察相关图可以看出,随着销售收入的增加,研究开发费用的平均水平不断提高,但离散程度也逐步扩大。这说明变量之间可能存在递增的异方差性。 (2 )残差图分析 首先对数据按照解释变量X 由小至大进行排序(SORT X),然后建立一元线性回归方程(LS Y C X)。 因此,模型估计式为: XY*0 3 2.05 0 7.1 8 7 ----------(*) (0.17) (2.88) R2=0.31 s.e.=2850 F=0.011 建立残差关于 X 的散点图,可以发现随着 X 增加,残差呈现明显的扩大趋势,表明存在递增的异方差。 2、Park 检验 建立回归模型(LS Y C X),结果如(*)式。 生成新变量序列: GENR LNE2 = LOG(RESID^2) GENR LNX = LOG(X) 生成新残差序列对解释变量的回归模型(LS LNE2 C LNX)。从下图所示的回归结果中可以看出,LNX 的系数估计值不为 0 且能通过显著性检验,即随机误差项的方差与解释变量存在较强的相关关系,即认为存在异方差性。 3、Gleis er 检验 建立回归模型(LS Y C X),结果如(*)式。 生成新变量序列: GENR E = ABS(RESID) 分别建立新残差序列 E 对各解释变量2121212/////XXXXXX的...