《流体力学》典型例题20111120

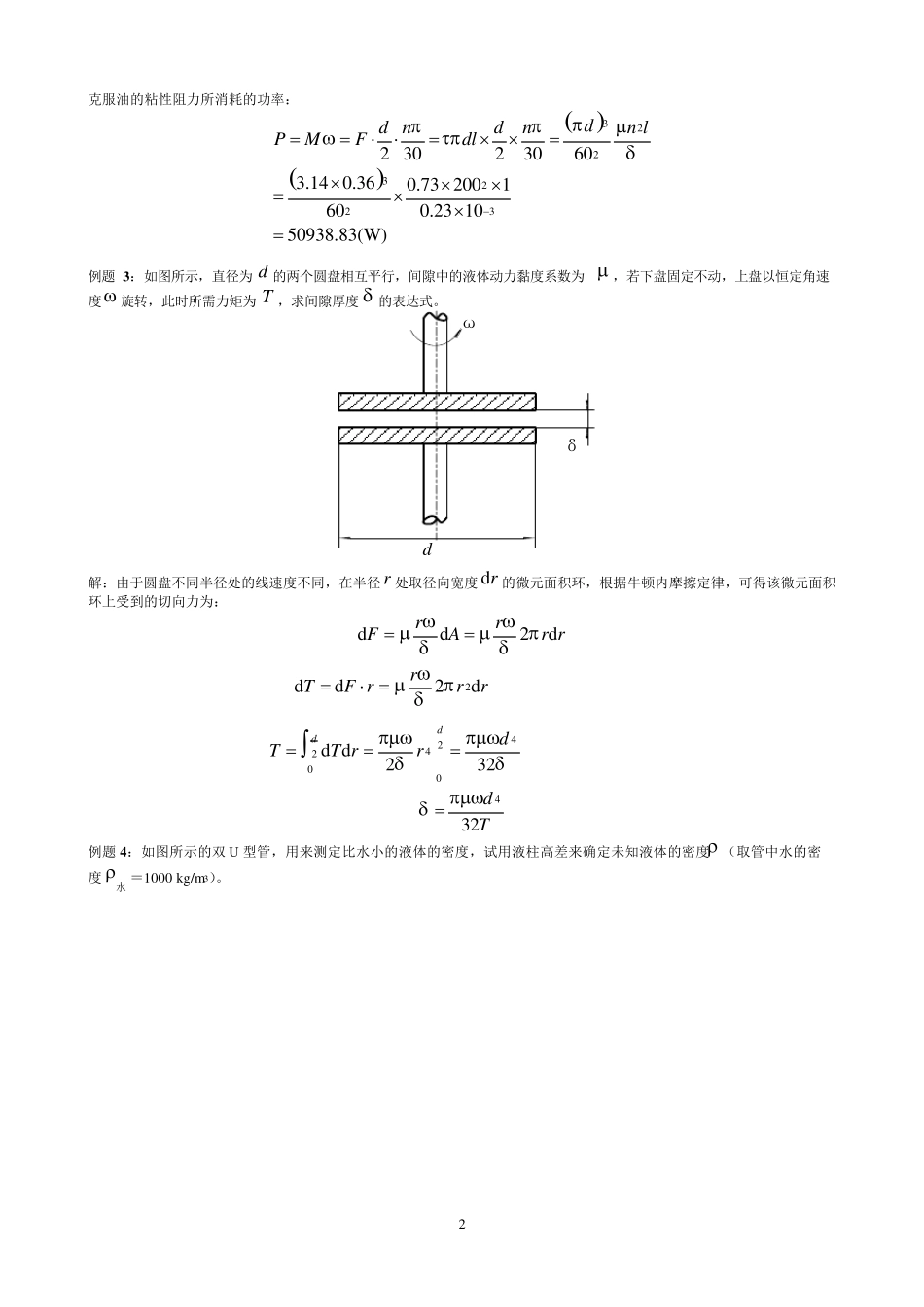
1 《流体力学》典型例题（ 9 大类） 例1~例3——牛顿内摩擦定律（牛顿剪切公式）应用 例4~例5——流体静力学基本方程式的应用——用流体静力学基本方程和等压面计算某点的压强或两点之间的压差。 例6~例8——液体的相对平衡——流体平衡微分方程中的质量力同时考虑重力和惯性力（补充内容） （1）等加速直线运动容器中液体的相对平衡（与坐标系选取有关） （2）等角速度旋转容器中液体的平衡（与坐标系选取有关） 例9——求流线、迹线方程；速度的随体导数（欧拉法中的加速度）；涡量计算及流动有旋、无旋判断 例10~16——速度势函数、流函数、速度场之间的互求 例17——计算流体微团的线变形率、角变形率及旋转角速度 例18~20——动量定理应用（课件中求弯管受力的例子） 例21~22——总流伯努利方程的应用 例23——综合：总流伯努利方程、真空度概念、平均流速概念、流态判断、管路系统沿程与局部损失计算 例题1：如图所示，质量为m＝5 kg、底面积为S＝40 cm×60 cm 的矩形平板，以U＝1 m/s 的速度沿着与水平面成倾角 ＝30 的斜面作等速下滑运动。已知平板与斜面之间的油层厚度 ＝1 mm，假设由平板所带动的油层的运动速度呈线性分布。求油的动力粘性系数。 UG=mg 解：由牛顿内摩擦定律，平板所受的剪切应力duUdy ＝ 又因等速运动，惯性力为零。根据牛顿第二定律：0mFa，即 ： gsin0mS  324gsin5 9.8 sin 301 100.1021 N s m1 40 60 10mU S   粘性是 流体在 运动状 态下，具 有的抵 抗 产 生 剪切变形速率能 力的量度；粘性是 流体的一 种 固 有物 理属 性； 流体的粘性具有传 递 运动和阻 滞 运动的双 重 性。 例题2：如图所示，转轴 的直径 d＝0.36 m，轴 承 的长 度l＝1 m，轴 与轴 承 的缝 隙 宽 度 ＝0.23 mm，缝 隙 中充 满 动力粘性系数0.73Pa s 的油，若 轴 的转速200rpmn 。求克 服 油的粘性阻 力所消 耗 的功 率。 dln 解：由牛顿内摩擦定律，轴 与轴 承 之间的剪切应力 60ddn duy＝ 粘性阻 力（摩擦力）：FSdl  2 克服油的粘性阻力所消耗的功率： 32232232 30230603.14 0.360.73 2001600.23 1050938.83(W)dd ndnn lPMFdl 例题3：...