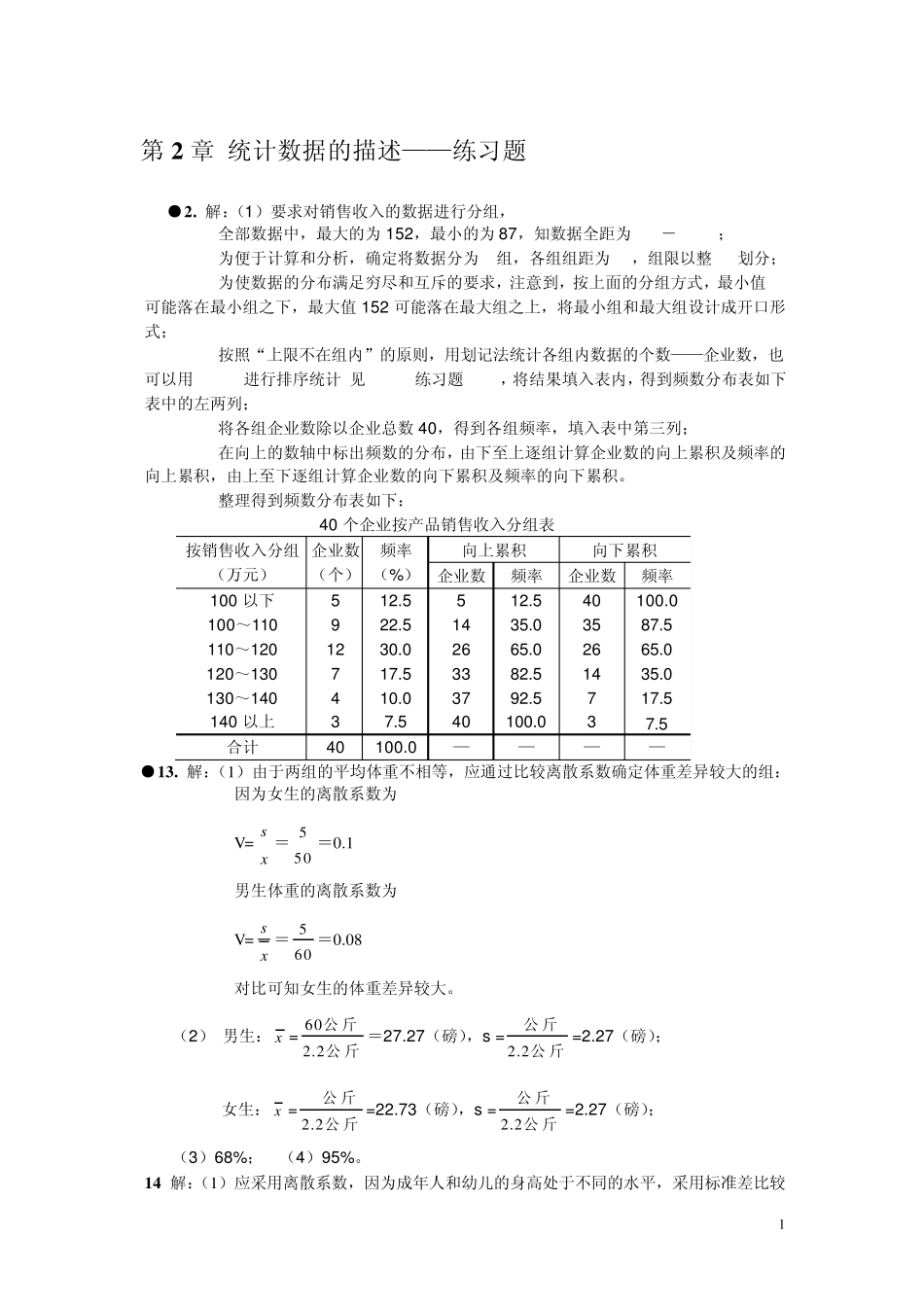
1 第2 章 统计数据的描述——练习题 ●2 . 解:(1)要求对销售收入的数据进行分组, 全部数据中,最大的为 152,最小的为 87,知数据全距为 152-87=65; 为便于计算和分析,确定将数据分为 6组,各组组距为 10,组限以整 10划分; 为使数据的分布满足穷尽和互斥的要求,注意到,按上面的分组方式,最小值 87可能落在最小组之下,最大值 152 可能落在最大组之上,将最小组和最大组设计成开口形式; 按照“上限不在组内”的原则,用划记法统计各组内数据的个数——企业数,也可以用 Excel进行排序统计(见 Excel练习题 2.2),将结果填入表内,得到频数分布表如下表中的左两列; 将各组企业数除以企业总数40,得到各组频率,填入表中第三列; 在向上的数轴中标出频数的分布,由下至上逐组计算企业数的向上累积及频率的向上累积,由上至下逐组计算企业数的向下累积及频率的向下累积。 整理得到频数分布表如下: 40 个企业按产品销售收入分组表 按销售收入分组 (万元) 企业数 (个) 频率 (%) 向上累积 向下累积 企业数 频率 企业数 频率 100 以下 100~110 110~120 120~130 130~140 140 以上 5 9 12 7 4 3 12.5 22.5 30.0 17.5 10.0 7.5 5 14 26 33 37 40 12.5 35.0 65.0 82.5 92.5 100.0 40 35 26 14 7 3 100.0 87.5 65.0 35.0 17.5 7.5 合计 40 100.0 — — — — ●1 3 . 解:(1)由于两组的平均体重不相等,应通过比较离散系数确定体重差异较大的组: 因为女生的离散系数为 V= sx= 550=0.1 男生体重的离散系数为 V= sx= 560=0.08 对比可知女生的体重差异较大。 (2) 男生: x = 602.2公 斤公 斤=27.27(磅),s =2.25公 斤公 斤=2.27(磅); 女生: x =2.250公 斤公 斤=22.73(磅),s =2.25公 斤公 斤=2.27(磅); (3)68%; (4)95%。 1 4 解:(1)应采用离散系数,因为成年人和幼儿的身高处于不同的水平,采用标准差比较 2 不合适。离散系数消除了不同组数据水平高低的影响,采用离散系数就较为合理。 (2)利用Ex cel 进行计算,得成年组身高的平均数为172.1,标准差为4.202,从而得: 成年组身高的离散系数:024.01.1722.4sv; 又得幼儿组身高的平均数为71.3,标准差为2.497,从而得: 幼儿组身高的离散系数:2.4970.03571.3sv; 由于幼儿组身高的离散系数大于成年组...