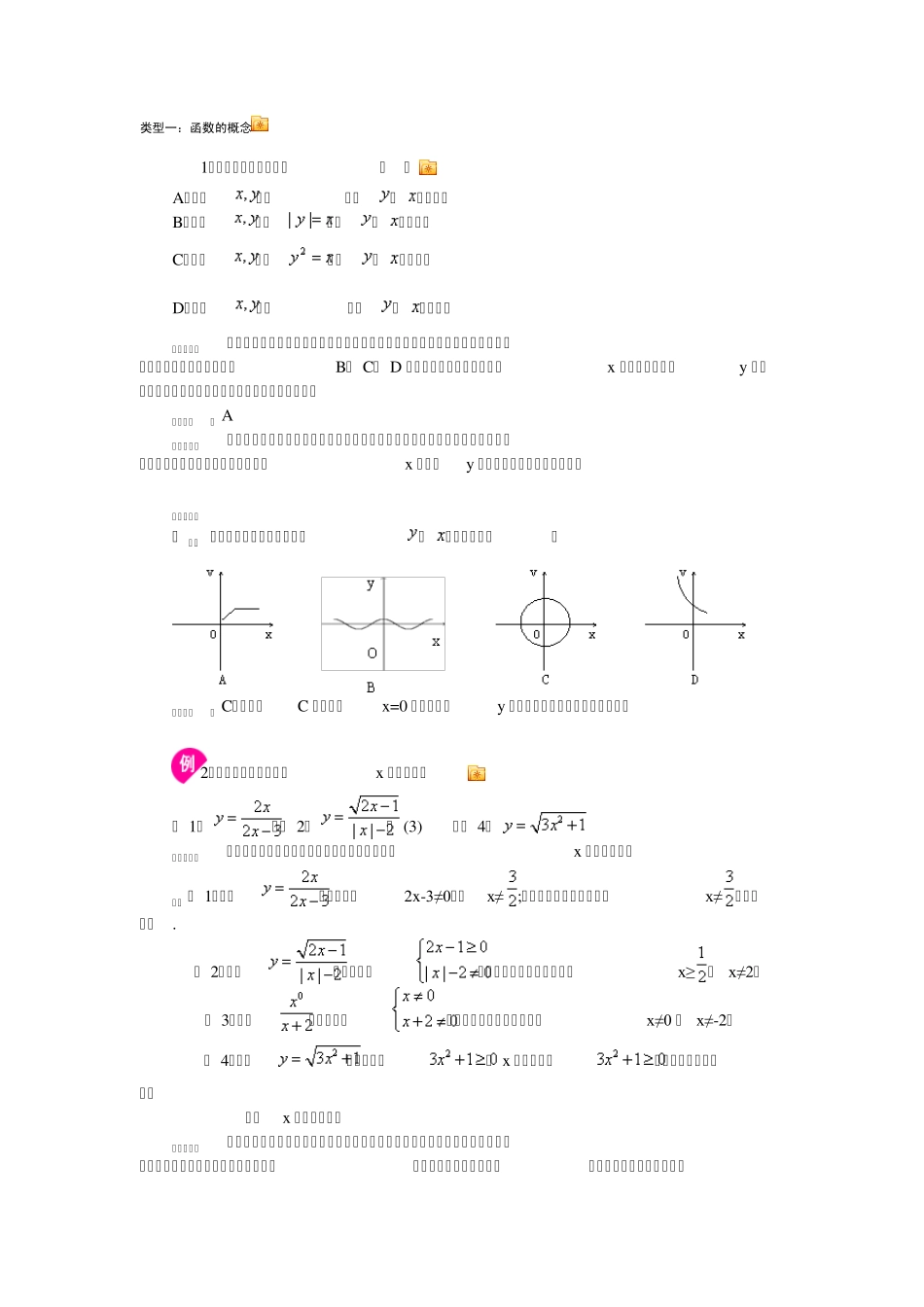
类型一:函数的概念 1、下列说法正确的是: ( ) A.变量满足,则是的函数; B.变量满足,则是的函数; C.变量满足,则是的函数; D.变量满足,则是的函数; 思路分析:理解函数的概念,关键是函数与自变量之间是单值对应关系,自变量的值确定后,函数值是唯一确定的。B、 C、 D 三个选项,对于一个确定的x的值,都有两个y值和它对应,不满足单值对应的条件,所以不是函数。 【答案】: A 总结升华:不管函数是用解析式表示的,还是列表法,图象法表示的,关键看函数与自变量之间是单值对应关系,对于每一个x的值,y都有唯一确定的值和它对应。 举一反三: 【 变式 】下列图形中的曲线不表示是的函数的是( ) 【答案】: C;提示:C 答案对于x=0 时,有两个y值和它对应,不满足函数的定义。 2、求下列函数中自变量x的取值范围 ( 1);( 2); (3);( 4) 思路点拨:函数中自变量的取值范围,是使解析式有意义的x的取值范围。 解: ( 1)要使有意义,需2x-3≠0,即x≠;所以自变量的取值范围是x≠ 的一切实数. ( 2)要使有意义,需,所以自变量的取值范围是x≥ 且 x≠2。 ( 3)要使有意义,需,所以自变量的取值范围是x≠0 且 x≠-2。 ( 4)要使有意义,需, x为一切实数,所以自变量的取值范 围是x为一切实数。 总结升华:当解析式是整式时,自变量的取值范围是全体实数;当解析式是分式时,自变量的取值范围是使分母不为零的实数;当解析式是二次根式时,自变量的取值范围是使被开方数不小于零的实数;当解析式中含有零指数幂或负整数指数幂时,自变量的取值应使相应的底数不为零;当解析式表示实际问题时,自变量的取值必须使实际问题有意义。 举一反三: 【 变式 】( 2011 湖南衡阳)函数中自变量x的取值范围是( ) A.≥- 3 B.≥- 3 且 C. D.且 【 答案 】 B 类型二:求一次函数的解析式 3、已知一次函数图象经过点(3,-3),并且与x 轴交于点,求此函数的解析式。 思路点拨:一次函数解析式的一般形式y= kx+ b中含有两个待定系数,因此需要知道图象上两个点的坐标,才能确定k和 b,将点(3,-3), 代入y= kx+ b求解。 解: 设此一次函数关系式为y= kx+ b,① 将 (3,-3)和分别代入①,得 解得 ∴ 此函数解析式为y=-x+ 1. 举一反三: 【变式1】 若 y- 2 与 x+ 2 成正比例,且x= 0 时,y= 6,写出y与 x之...