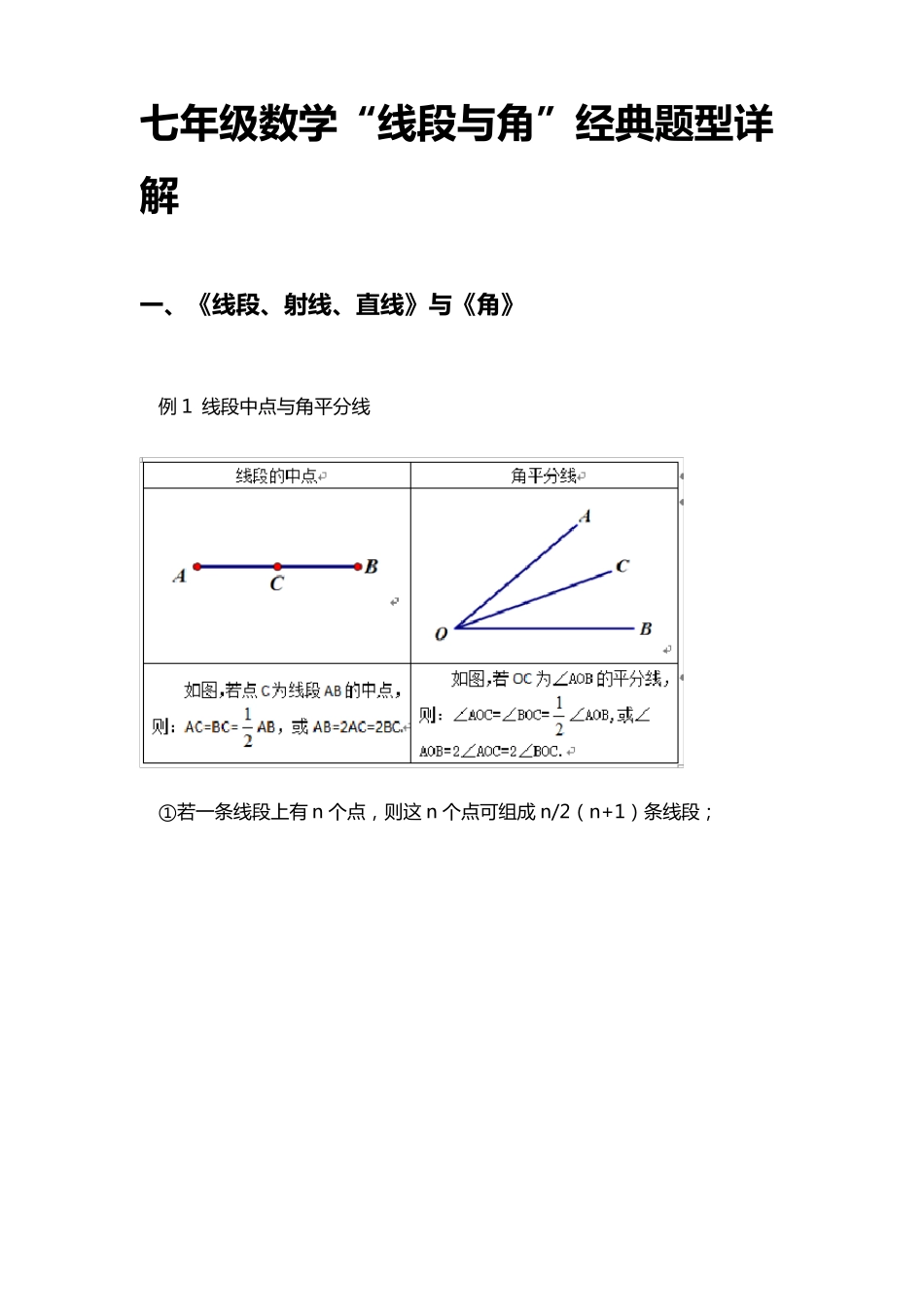
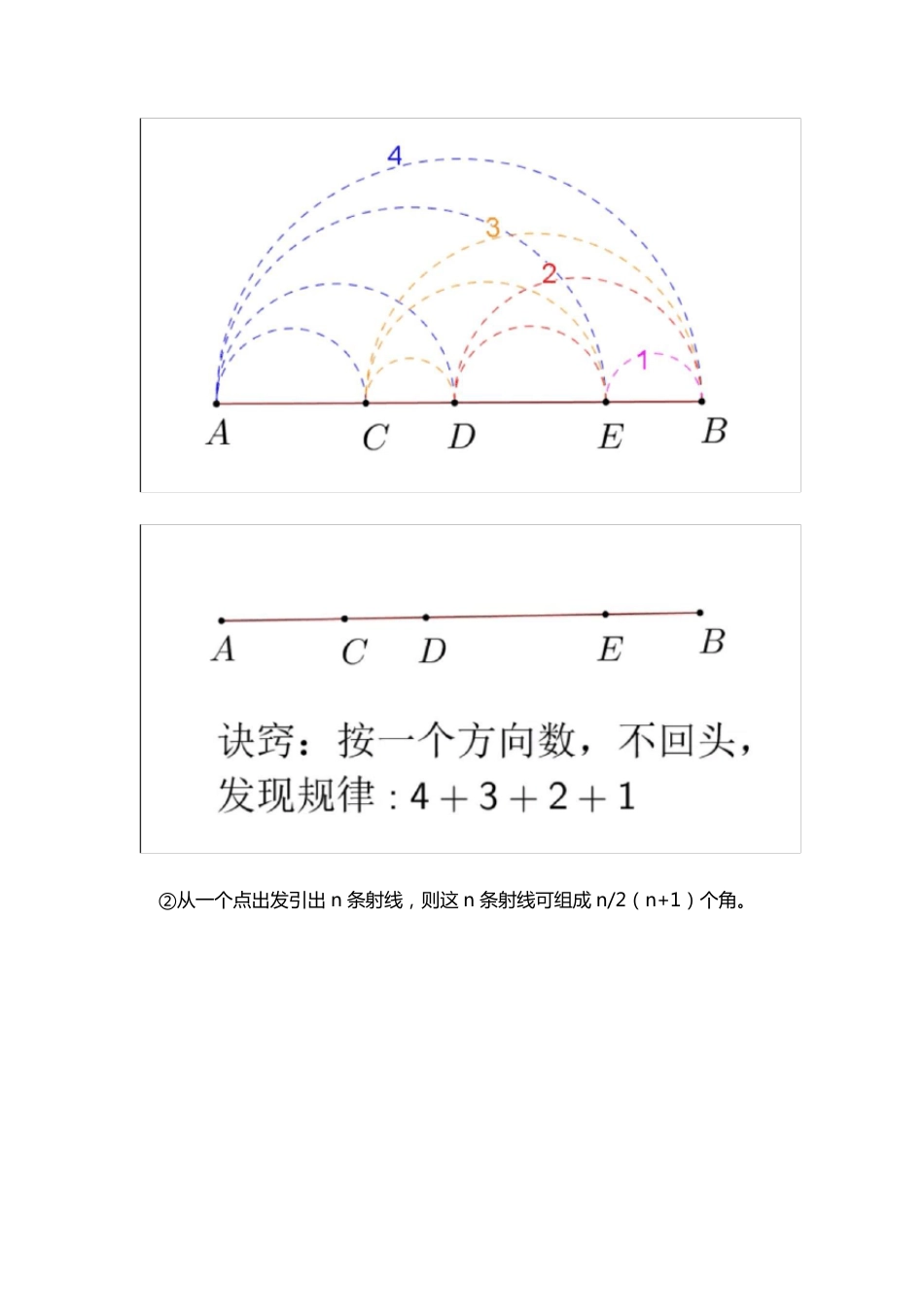
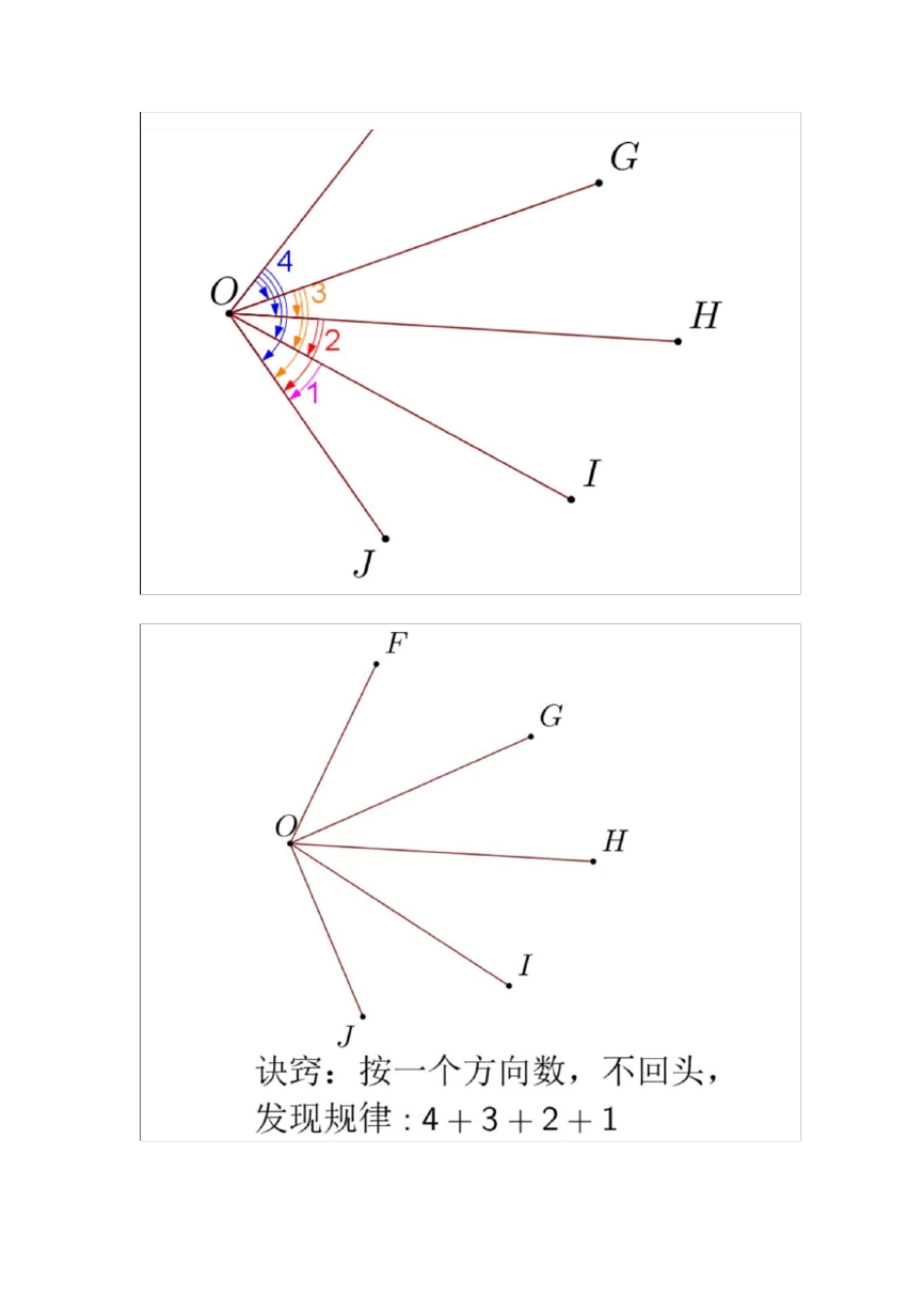
七 年 级 数 学 “线段与角”经典题型详解 一、《线段、射线、直线》与《角》 例 1 线 段 中 点 与 角 平 分 线 ①若一条线 段 上有 n 个点 ,则这 n 个点 可组成 n/2(n+1)条线 段 ; ②从一个点出发引出 n 条射线,则这 n 条射线可组成 n/2(n+1)个角。 例 2 线 段 类 与角类 多解问题 例 3 双中点问题与双角平分线 问题(1) 例 4 双 中 点 问 题 与双 角平分线问 题 (2) 例 5 数 线 段 条 数 与角的个数 二 、行程问题与钟面角问题 例 6 追击类问题(1) 例 7 追击类问题(2) 二 、 六 道 题 突 破 “线段与角”所有难题 1、 方程思想 例 1: 已 知 ∠AOB= 160°, ∠COE= 80°, OF 平 分∠AOE. ( 1) 如 图 1, 若 ∠COF= n°, 则 ∠BOE= ______°, ∠BOE 与 ∠COF 的 数 量 关 系 为_______; ( 2) 当 射 线 OE 绕 点 O 逆 时 针 旋 转 到 如 图 2 的 位 置 时 , ( 1) 中 ∠BOE与 ∠COF 的 数 量 关 系 是 否 仍 然 成 立 ? 请 说 明 理 由 ; ( 3) 在 ( 2) 的 条 件 下 , 如图 3, 在 ∠BOE 的 内 部 是 否 存 在 一 条 射 线 OD, 使 得 ∠BOD 为 直 角 , 且 ∠DOF=3∠DOE? 若 存 在 , 请 求 出 ∠COF 的 度 数 ; 若 不 存 在 , 请 说 明 理 由 . 分析: (1)(2)根 据 ∠EOC 和 ∠COF 的 度 数 , 可 以 求 出 ∠FOE 的 度 数 , 从 而 可 求 ∠AOE 的度 数 , 从 而 将 ∠AOB 的 度 数 减 去 ∠AOE 的 度 数 , 就 是 ∠BOE 的 度 数 , 若 将 ∠EOF的 度 数 用 n 来 表 示 , 或 将 位 置 改 变 , 方 法 也 是 不 变 的 . (3)要 求 ∠COF 的 度 数 ,只 需 求 出 ∠EOF 的 度 数 , 用 ∠COE 的 度 数 相 减 即 可 . 而 要 求 ∠EOF 的 度 数 , 我 们可 以 借 助 ∠DOF= 3∠DOE 的 条 件 , 最 后 , 利 用 ∠AOD+ ∠BOD= 160°, 建 立 方程 . 解答: (1)设 ∠COF= n°, ∠FOE= ∠COE- ∠COF= (80- n)°, OF 平 分 ∠AOE, ∴∠AOE= 2∠FOE= (160- 2n)°,∴∠BOE= ∠AOB- ∠AOE = ...