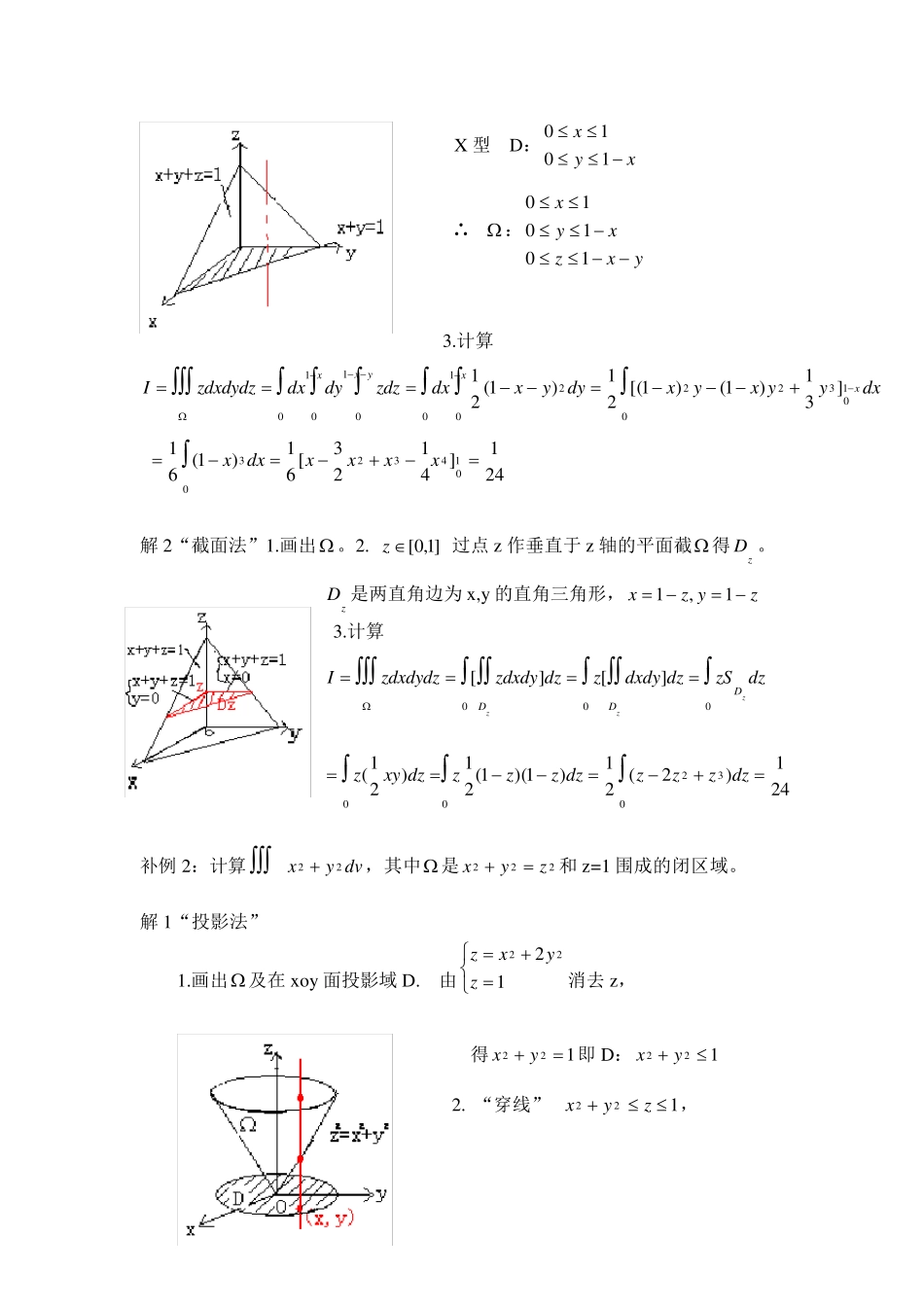
三重积分的计算方法介绍: 三重积分的计算是化为三次积分进行的。其实质是计算一个定积分(一重积分)和一个二重积分。从顺序看: 如果先做定积分21),,(zzdzzyxf,再做二重积分DdyxF),(,就是“投影法”,也即“先一后二”。步骤为:找及在 xoy 面投影域 D。多 D上一点(x,y)“穿线”确定z 的积分限,完成了“先一”这一步(定积分);进而按二重积分的计算步骤计算投影域 D 上的二重积分,完成“后二”这一步。ddzzyxfdvzyxfDzz 21]),,([),,( 如果先做二重积分zDdzyxf),,(再做定积分21)(ccdzzF,就是“截面法”,也即“先二后一”。步骤为:确定位于平面21czcz与之间,即],[21 ccz,过 z 作平行于 xoy 面的平面截,截面zD 。区域zD 的边界曲面都是z 的函数。计算区域zD 上的二重积分zDdzyxf),,(,完成了“先二”这一步(二重积分);进而计算定积分21)(ccdzzF,完成“后一”这一步。dzdzyxfdvzyxfccDz]),,([),,(21 当被积函数 f(z)仅为z 的函数(与 x,y 无关),且zD 的面积)(z容易求出时,“截面法”尤为方便。 为了简化积分的计算,还有如何选择适当的坐标系计算的问题。可以按以下几点考虑:将积分区域投影到 xoy 面,得投影区域 D(平面) (1) D 是X 型或 Y 型,可选择直角坐标系计算(当的边界曲面中有较多的平面时,常用直角坐标系计算) (2) D 是圆域(或其部分),且被积函数形如)(),(22xyfyxf时,可选择柱面坐标系计算(当为圆柱体或圆锥体时,常用柱面坐标计算) (3)是球体或球顶锥体,且被积函数形如)(222zyxf时,可选择球面坐标系计算 以上是一般常见的三重积分的计算方法。对向其它坐标面投影或不易作出的情形不赘述。 三重积分的计算方法小结: 1 .对三重积分,采用“投影法”还是“截面法”,要视积分域 及被积函数f(x,y,z)的情况选取。 一般地,投影法(先一后二):较直观易掌握; 截面法(先二后一): zD 是 在 z 处的截面,其边界曲线方程易写错,故较难一些。 特殊地,对zD 积分时,f(x,y,z)与 x,y 无关,可直接计算zDS。因而中只要],[baz, 且f(x,y,z)仅含 z 时,选取“截面法”更佳。 2 .对坐标系的选取,当 为柱体,锥体,或由柱面,锥面,旋转抛物面与其它曲面所围成的形体;被积函数为仅含 z 或)(22yxzf时,可考虑用柱面坐标计算...