东南大学信号与系统试题及答案

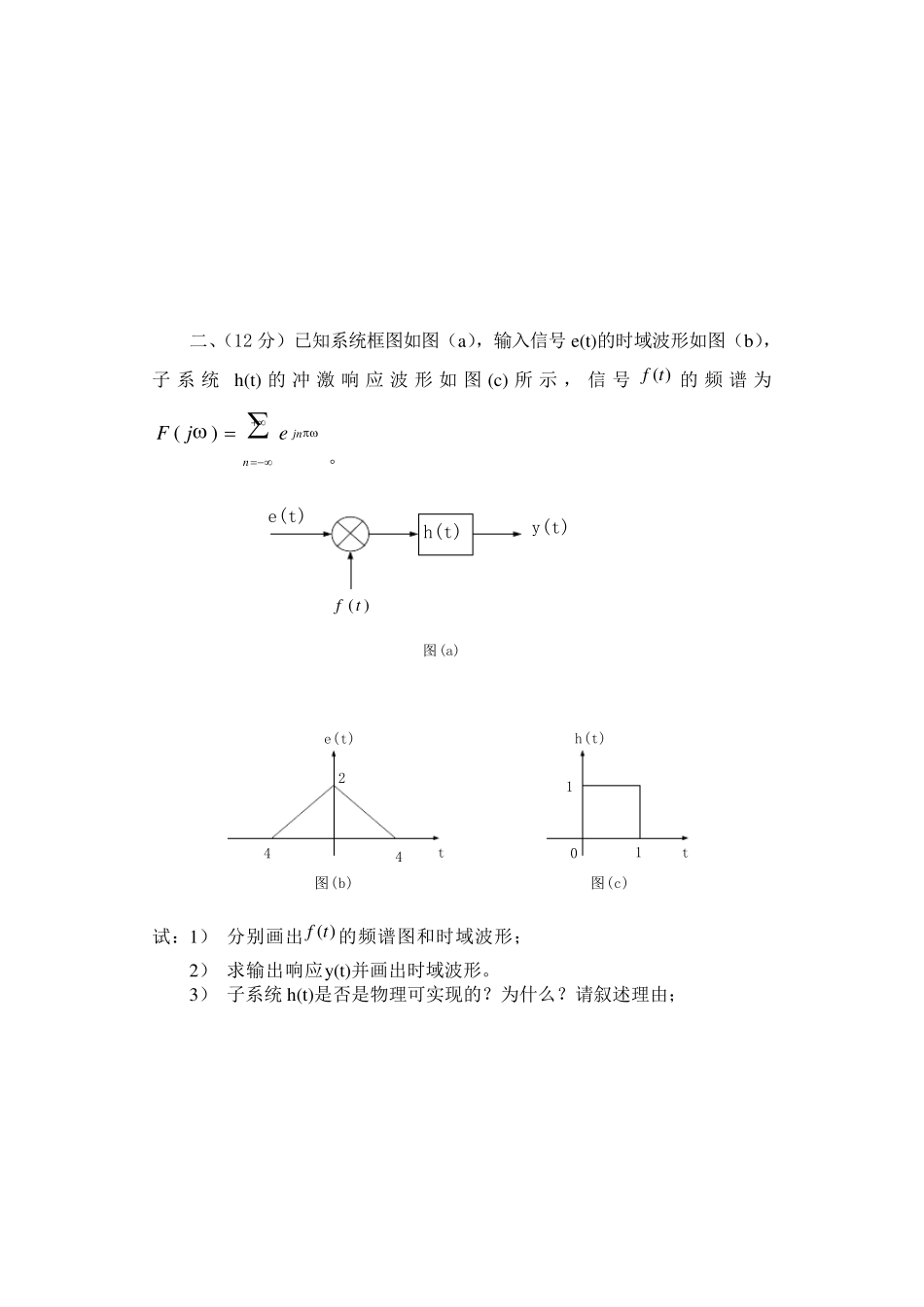
东 南 大 学 考 试 卷（A、B 卷） （答案附后） 课程名称 信号与线性系统 考试学期 03-04-3 得分 适用专业 四系，十一系 考试形 式 闭卷 考试时间长度 120 分钟 一、简单计算题（每题8 分）： 1、 已知某连续信号 ( )f t 的傅里叶变换为21()23F jj，按照取样间隔1T  对其进行取样得到离散时间序列( )f k ，序列( )f k 的 Z变换。 2、 求序列10( )1 ,2,1kf k和2( )1 cos( )2fkkk的卷积和。 3、 已知某双边序列的 Z 变换为21( )1092F zzz，求该序列的时域表达式( )f k 。 4 、 已知某连续系统的特征多项式为： 269111063)(234567ssssssssD 试判断该系统的稳定情况，并指出系统含有负实部、零实部和正实部的根各有几个？ 5 、 已知某连续时间系统的系统函数为：3232642( )21sssH ssss 。试给出该系统的状态方程。 6 、 求出下面框图所示离散时间系统的系统函数。 1z1z2-0.3)(ke)(kr-0.2 二、（12 分）已知系统框图如图（a），输入信号 e(t)的时域波形如图（b），子 系 统h(t) 的 冲 激 响 应 波 形 如 图 (c) 所 示 ， 信 号( )f t 的 频 谱 为()jnnFje 。 e(t)图(a)h(t)y(t))(tf e(t)244t图(b) h(t)t图(c)011 试：1） 分别画出)(tf的频谱图和时域波形； 2） 求输出响应y (t)并画出时域波形。 3） 子系统 h(t)是否是物理可实现的？为什么？请叙述理由； 三（12 分）、已知电路如下图所示，激励信号为)()(tte，在 t=0 和 t=1时测得系统的输出为1)0(y，5.0)1( ey。分别求系统的零输入响应、零状态响应、全响应、以及自然响应和受迫响应。 e(t)L=2HC=1FR1=2 R2=1 +y(t)_ 四(1 2 分)、已知某离散系统的差分方程为 )1()()1(3)2(2kekykyky 其初始状态为6)2(,2)1(ziziyy，激励)()(kke； 求：1） 零输入响应)(kyzi、零状态响应)(kyzs及全响应)(ky； 2） 指出其中的自由响应分量和受迫响应分量； 3） 判断该系统的稳定性。 五（12 分）、已知某离散时间系统的单位函数响应( )cos( )2kh kk。 1） 求其系统函数( )H z ； 2） 粗略绘出该系统的幅频特性； 3） 画出该系统的框图。 六、（10 分）请叙述并证明 z 变换...