传热学上机实验

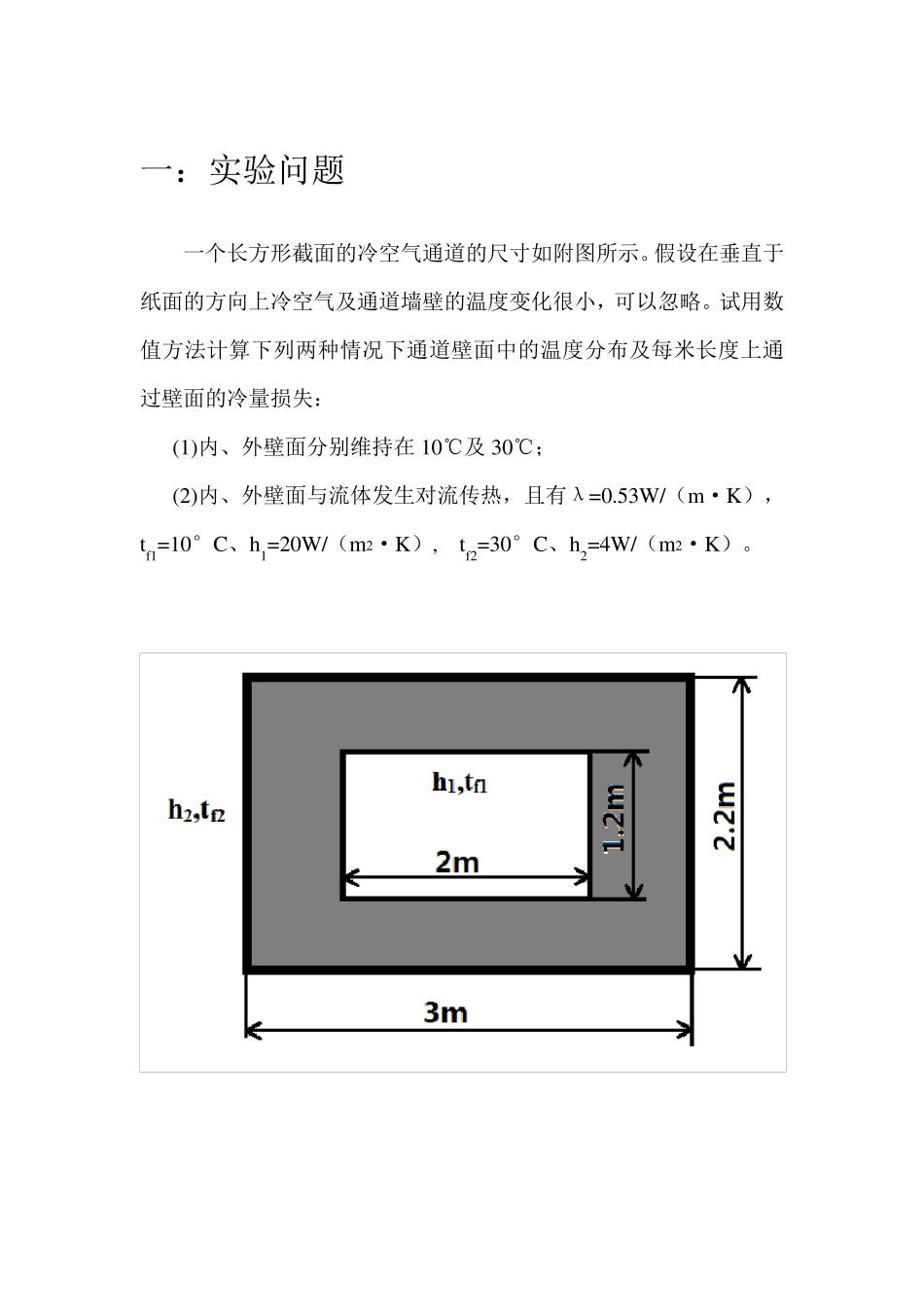
传热学上机实验 班级: 学号： 姓名： 一：实验问题 一个长方形截面的冷空气通道的尺寸如附图所示。假设在垂直于纸面的方向上冷空气及通道墙壁的温度变化很小，可以忽略。试用数值方法计算下列两种情况下通道壁面中的温度分布及每米长度上通过壁面的冷量损失： (1)内、外壁面分别维持在10℃及30℃； (2)内、外壁面与流体发生对流传热，且有λ=0.53W/（m·K），tf1=10°C、h1=20W/（m2·K）, tf2=30°C、h2=4W/（m2·K）。 二：问题分析与求解 本题采用数值解法，将长方形截面离散成31×23 个点，用有限个离散点的值的集合来代替整个截面上温度的分布，通过求解按傅里叶导热定律、牛顿冷却公式及热平衡法建立的代数方程，来获得整个长方形截面的温度分布，进而求出其通过壁面的冷量损失。 1 . 建立控制方程及定解条件 对于第一问，其给出了边界上的温度，属于第一类边界条件。 CCytxt301002222外壁温内壁温 对于第二问，其给出了边界上的边界上物体与周围流体间的表面传热系数h 及周围流体的温度 tf ，属于第三类边界条件。 fwwtthntytxt02222 2 . 确定节点（区域离散化） 用一系列与坐标轴平行的网格线把长方形截面划分为 31×23 个节点。则步长为 0.1m，记为△x =△y =0.1m。 3 . 建立节点物理量的代数方程 对于第一问有如下离散方程： 代表内部点,，点4126~6,1018,26~6,106,18~6,10,2618~6,10,631~1,3023,31~1,301,23~1,30,3123~1,30,11,1,,1,1,nmtttttnCmtnCmtnCntnCntnCmtnCmtnCntnCntnmnmnmnmnm 对于第二问有如下离散方程： 对于外部角点（1 ,1 ）、（1 ,2 3 ）、（3 1 ,1 ）、（3 1 ,，2 3 ）有： 02222,1,,22,,1,22xyttttxhyxttttyhnmnmnmfnmnmnmf 得到：2 2,3 12 3,3 02 3,3 12,3 11,3 01,3 12 2,12 3,22 3,12,11,21,11 8 65 33 14 0 01 8 65 33 14 0 01 8 65 33 14 0 01 8 65 33 14 0 0tttttttttttt 同理可得： 对于内部角点（6 ,6 ）（6 ,1 8 ）（2 6 ,6 ）（2 6 ,1 8 ...