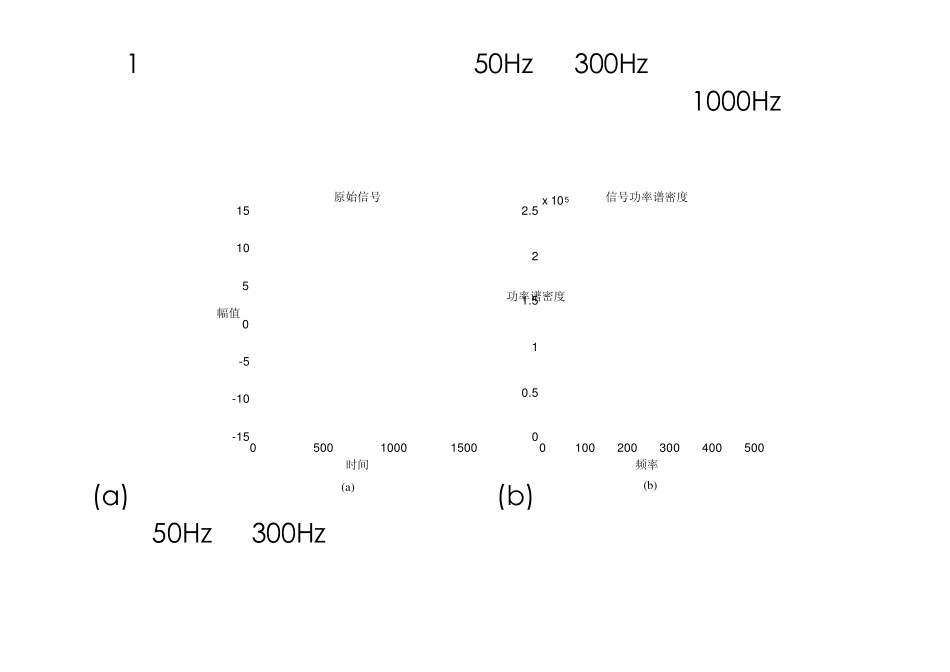
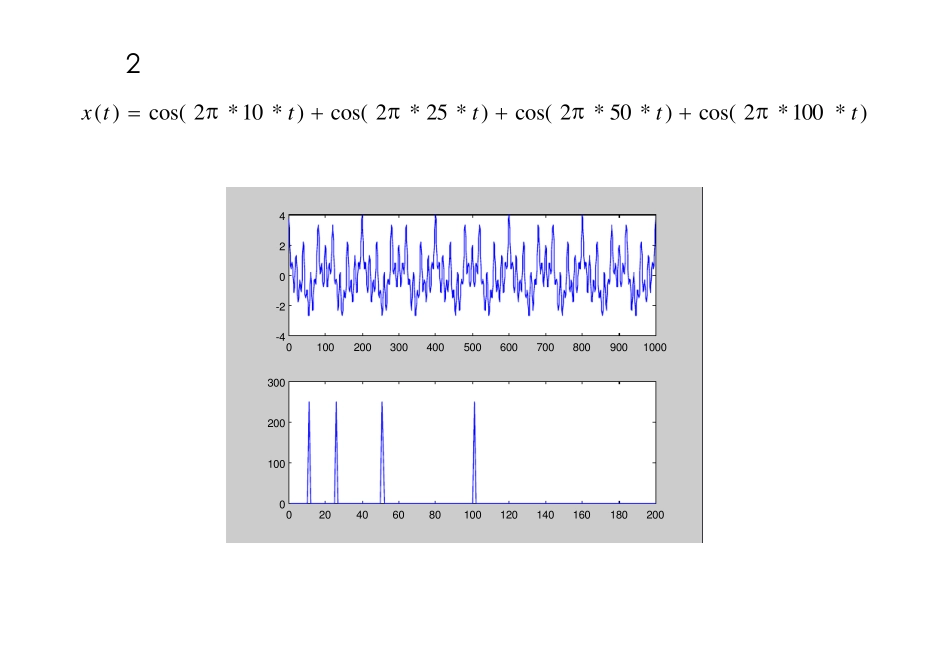
傅立叶变换与短时傅立叶变换 为了分析和处理非平稳信号,人们对傅立叶分析进行了推广乃至根本性的革命,提出并发展了一系列新的信号分析理论: 短时傅立叶变 Gabor变换 时频分析 小波变换 Randon-Wiger 变换 分数阶傅立叶变换 线调频小波变换 循环统计理论和调幅-调频信号分析 ‥‥‥ 举例 1 有一信号主要频率成分是 50Hz和 300Hz的正弦信号,该信号被一白噪声污染,现对该信号进行采样,采样频率为 1000Hz,通过傅立叶变换对其频率成分进行分析。 从(a)中看不出任何频率的性质,但从(b)中可以明显地看出该信号是由频率为 50Hz和 300Hz的正弦信号和频率分布广泛的白噪声信号组成。 0 500 1000 1500 -15 -10 -5 0 5 10 15 幅值 时间 原始信号 0 100 200 300 400 500 0 0.5 1 1.5 2 2.5 x 10 5 功率谱密度 频率 信号功率谱密度 (a) (b) 举例 2 一个静态信号有如下形式 )*100*2cos()*50*2cos()*25*2cos()*10*2cos()(tttttx 其原始信号和傅立叶变换如下: 01 0 02 0 03 0 04 0 05 0 06 0 07 0 08 0 09 0 01 0 0 0-4-202402 04 06 08 01 0 01 2 01 4 01 6 01 8 02 0 001 0 02 0 03 0 0另一个信号:在 0 到 300ms之间为100Hz 的正弦信号,在 300 到 600ms之间为 50Hz 的信号,在 600 到 800ms 之间为 25Hz 的信号,在 800到 1000ms 之间为 10Hz 的信号,其原始信号和傅立叶变换如下图: 比较两幅图可以看出,两个信号的功率频谱图基本相同。 01 0 02 0 03 0 04 0 05 0 06 0 07 0 08 0 09 0 01 0 0 0-1-0 .500 .5102 04 06 08 01 0 01 2 01 4 01 6 01 8 02 0 0051 01 52 02 5短时傅立叶变换 Dennis Gabor 于 1946 年引入了短时傅立叶变换(Short-time Fou rier Transform)。短时傅立叶变换的基本思想是:把信号分成许多小的时间隔,用傅立叶变换分析每一个时间间隔,以便确定该时间间隔存在的频率。其表达式为: .)()(),(dtetgtfStif 其中,)(tg为一窗口函数,它一般是一光滑的低通函数,只在τ的附近有值,在其余处迅速衰减掉。这样,我们便得到函数在时刻τ附近的频率信息(即:频率为ω的信号成分的相对含量)。随着时间τ的变化,)(tg所确定的窗函数在时间轴上移动,对)(tf逐渐进行分析。 这样信号在窗函数上的展开...