傅里叶变换的基本性质

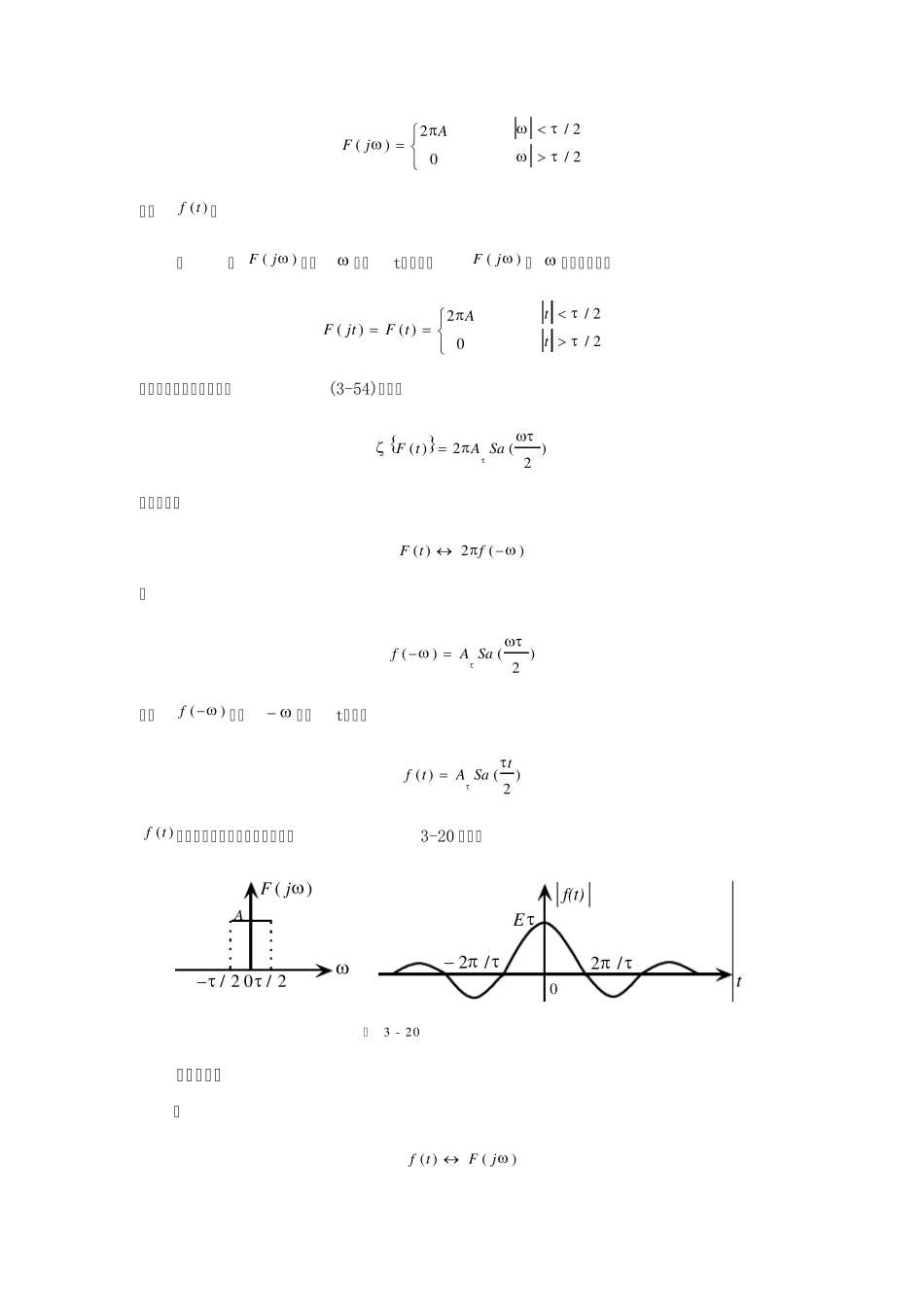
3-5 傅里叶变换的基本性质 傅里叶变换建立了时间函数和频谱函数之间转换关系。在实际信号分析中，经常需要对信号的时域和频域之间的对应关系及转换规律有一个清楚而深入的理解。因此有必要讨论傅里叶变换的基本性质，并说明其应用。 一、 线性 傅里叶变换是一种线性运算。若 )()(11jFtf )()(22jFtf 则 )()()()(2121jbFjaFtbftaf (3-55) 其中a 和 b 均为常数，它的证明只需根据傅里叶变换的定义即可得出。 例 3-6 利用傅里叶变换的线性性质求单位阶跃信号的频谱函数)( jF。 解 因 )sgn(2121)()(ttUtf 由式(3-55)得 jjttUjF1)(221)(221)sgn(21121)()( 二、对称性 若 )()(jFtf )(2)(fjtF (3-56) 证明 因为  dejFtftj)(21)( 有  dejFtftj)()(2  dejFtftj)()(2 将上式中变量 换为x，积分结果不变，即 dxejxFtfjx t)()(2  再将t 用  代之，上述关系依然成立，即 dxejxFfxj)()(2 最后再将x 用 t 代替，则得 )()()(2jtFdtejtFftj 所以 )(2)(fjtF 证毕 若)(tf是一个偶函数，即)()(tftf，相应有)()(ff，则式(3-56)成为 )(2)(fjtF (3-57) 可见，傅里叶变换之间存在着对称关系，即信号波形与信号频谱函数的波形有着互相置换的关系，其幅度之比为常数2。 式中的表示频谱函数坐标轴必须正负对调。例如 1)()()(jFttf (2)(21)(fjtF 例 3-7 若信号)(tf的傅里叶变换为 02)(AjF 2/2/ 试求)(tf。 解 将)( jF中的 换成t，并考虑)( jF为  的实函数，有 02)()(AtFjtF 2/2/tt 该信号的傅里叶变换由式(3-54)可知为 )2(2)( SaAtF 根据对称性 )(2)(ftF 故 )2()( SaAf 再将)( f中的换成t，则得 )2()(tSaAtf )(tf为抽样函数，其波形和频谱如图3-20 所示。 图 3 - 2 0)( jFA2/02/f(t)0t E /2 /2 三、折叠性 若 )()(jFtf 则 )()()()(jFjFjFtf 为虚函数为实函数)()(tftf (3-58) 四、尺度变换...