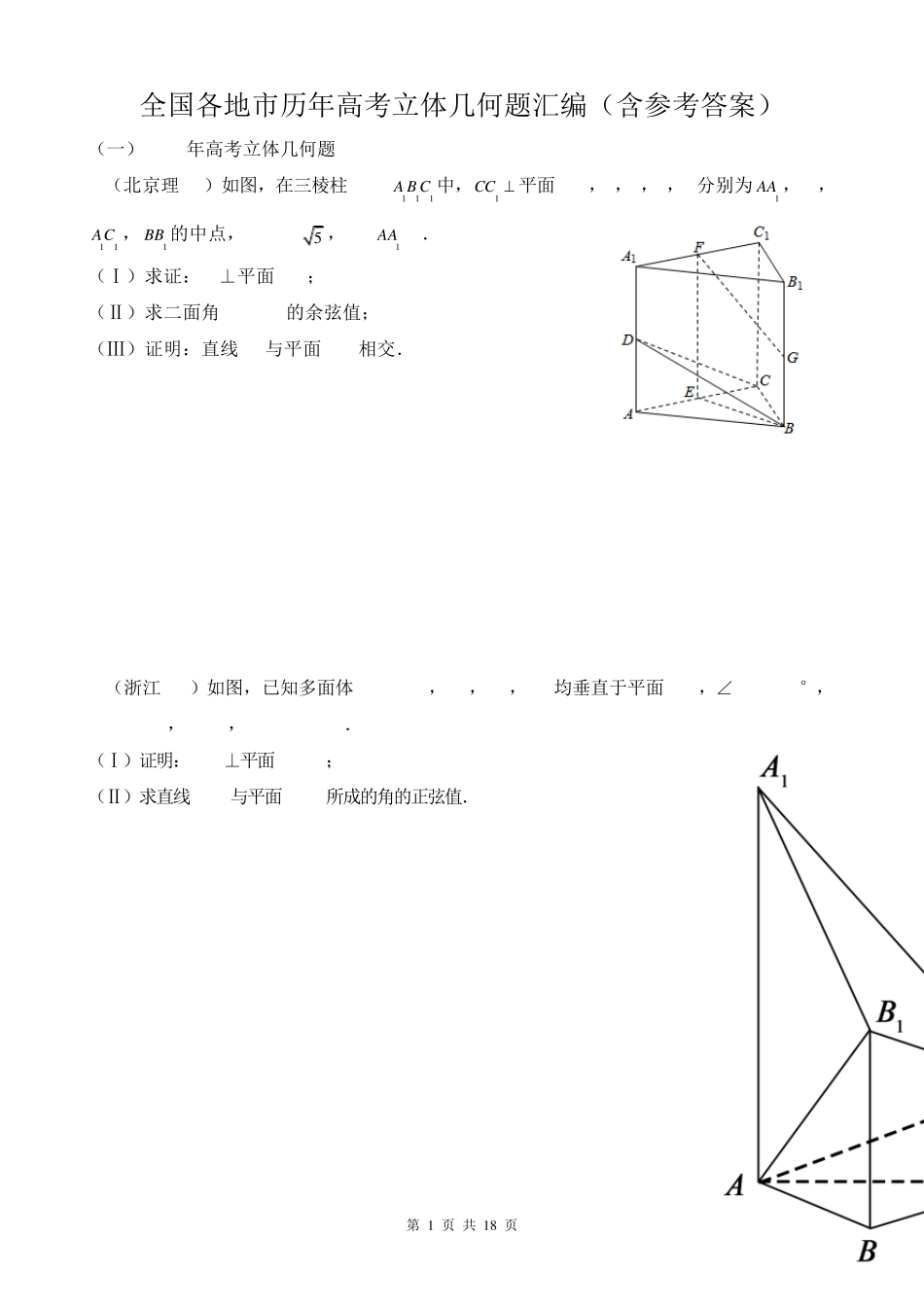
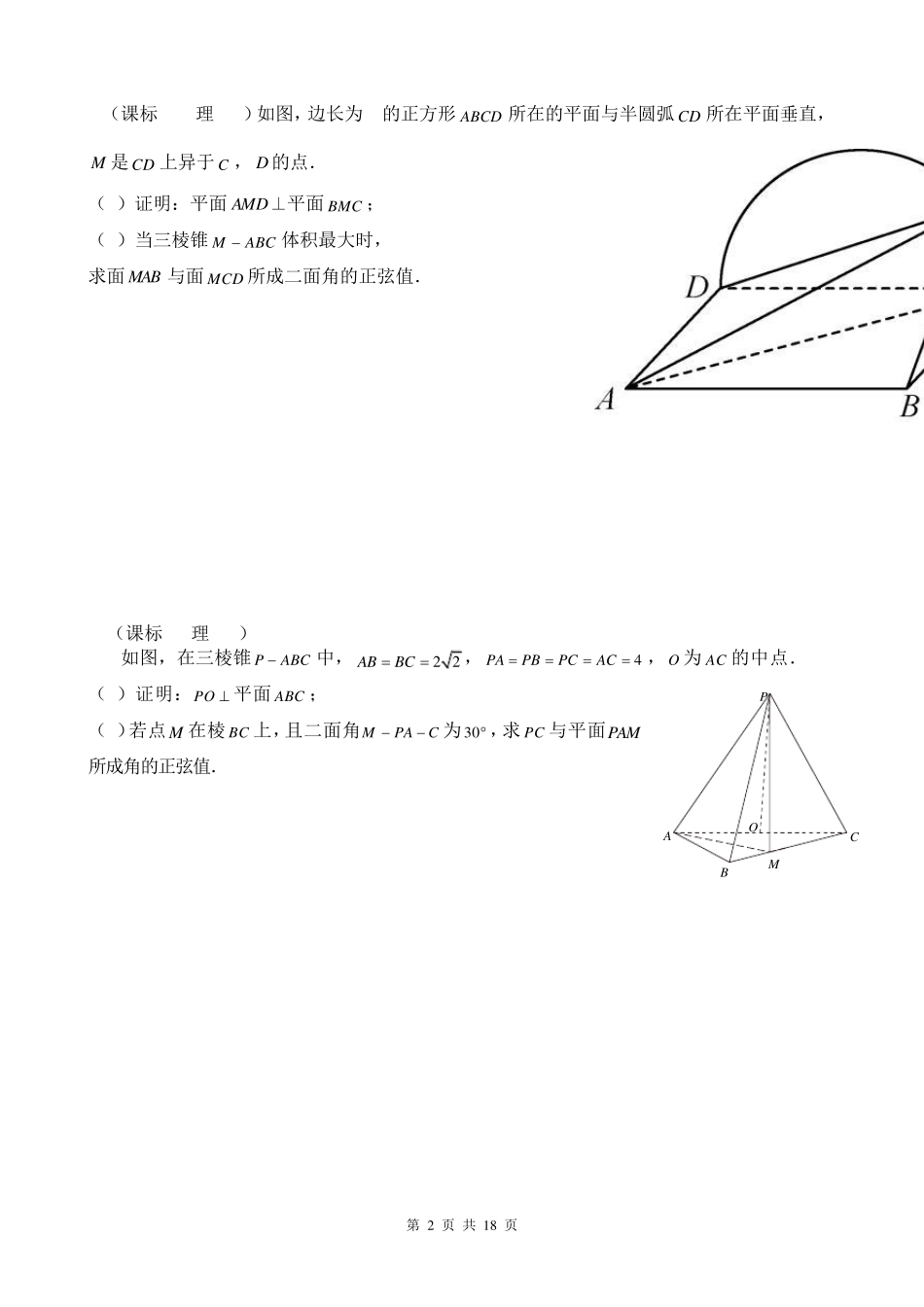
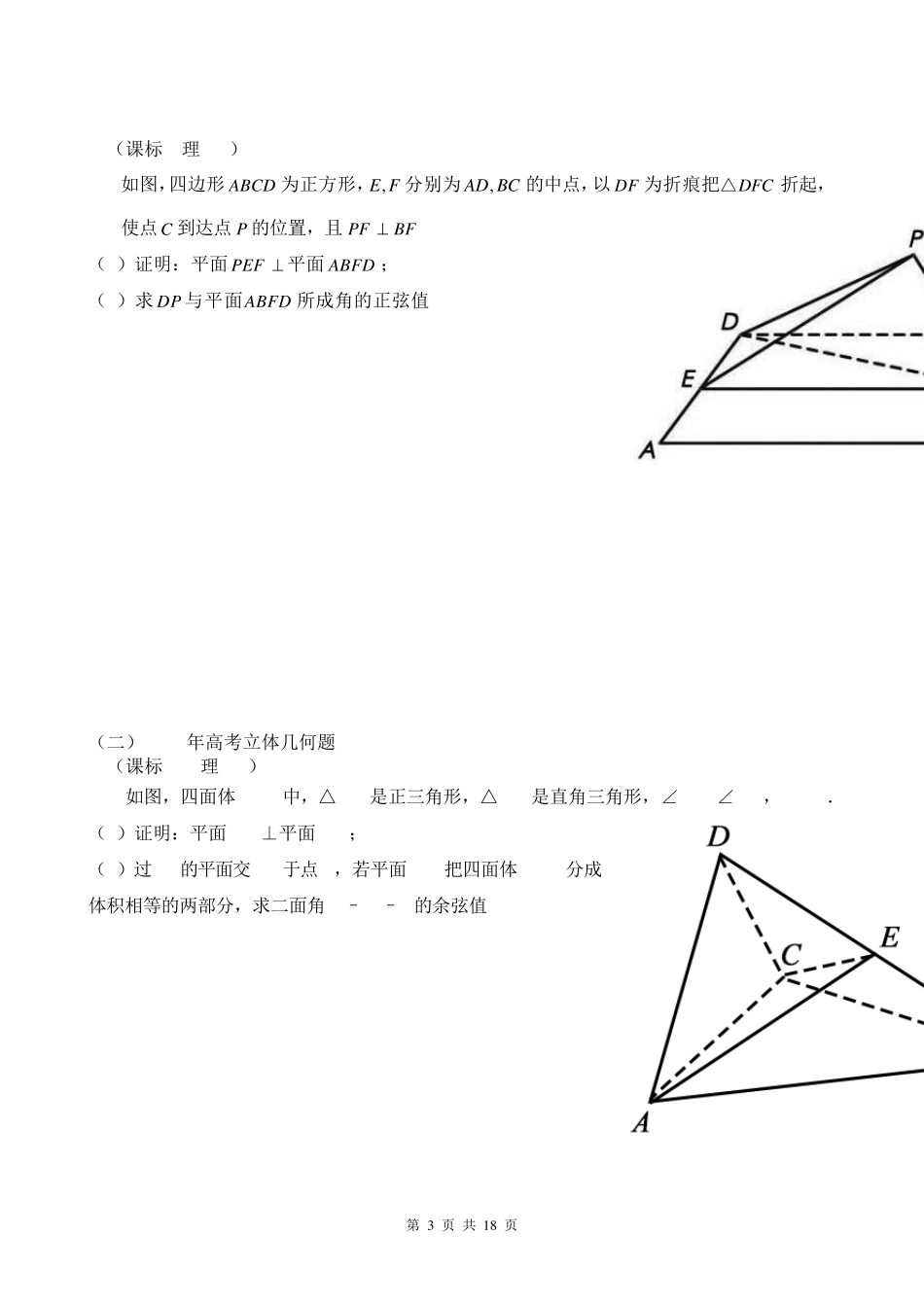
第 1 页 共 1 8 页 全国各地市历年高考立体几何题汇编(含参考答案) (一)2018年高考立体几何题 1.(北京理16)如图,在三棱柱ABC-111A B C 中,1CC 平面ABC,D,E,F,G分别为1AA ,AC,11AC ,1BB 的中点,AB=BC= 5 ,AC=1AA =2. (Ⅰ)求证:AC⊥平面BEF; (Ⅱ)求二面角B-CD-C1的余弦值; (Ⅲ)证明:直线FG与平面BCD相交. 2.(浙江-19)如图,已知多面体ABCA1B1C1,A1A,B1B,C1C均垂直于平面ABC,∠ABC=120°,A1A=4,C1C=1,AB=BC=B1B=2. (Ⅰ)证明:AB1⊥平面A1B1C1; (Ⅱ)求直线AC1与平面ABB1所成的角的正弦值. 第 2 页 共 1 8 页 3.(课标III理-19)如图,边长为2的正方形所在的平面与半圆弧所在平面垂直,是上异于,的点. (1)证明:平面 平面; (2)当三棱锥体积最大时, 求面与面所成二面角的正弦值. 4.(课标II理-20) 如图,在三棱锥PABC中,22ABBC,4PAPBPCAC,O 为AC 的中点. (1)证明:PO 平面ABC ; (2)若点M 在棱BC 上,且二面角MPAC为3 0 ,求PC 与平面PAM所成角的正弦值. ABCDCDMCDCDAMD⊥BMCMABCMABMCDPAOCBM 第 3 页 共 1 8 页 5.(课标I理-18) 如图,四边形ABCD 为正方形,,E F分别为,AD BC 的中点,以DF 为折痕把DFC△折起,使点C 到达点P的位置,且PFBF. (1)证明:平面PEF 平面ABFD ; (2)求DP与平面ABFD 所成角的正弦值. (二)2017年高考立体几何题 1.(课标III理-19) 如图,四面体ABCD中,△ABC是正三角形,△ACD是直角三角形,∠ABD=∠CBD,AB=BD. (1)证明:平面ACD⊥平面ABC; (2)过AC的平面交BD于点E,若平面AEC把四面体ABCD分成体积相等的两部分,求二面角D–AE–C的余弦值. 第 4 页 共 1 8 页 2.(课标II理-19) 如图,四棱锥P-ABCD中,侧面PAD为等边三角形且垂直于底面ABCD,o1,9 0 ,2ABBCADBADABC E是PD的中点. (1)证明:直线CE∥平面PAB; (2)点M在棱PC 上,且直线BM与底面ABCD所成角为o4 5 ,求二面角MABD的余弦值. 3.(课标I理-18)如图,在四棱锥P− ABCD中,AB//CD,且9 0BAPCDP . (1)证明:平面PAB⊥平面PAD; (2)若 PA=PD=AB=DC,9 0APD,求二面角A− PB− C的余弦值. 第 5 页 共 1 8 页 (三)2016年高考立体几何题 1.(课标III理-19) 如图,四棱锥中,地面,,,...