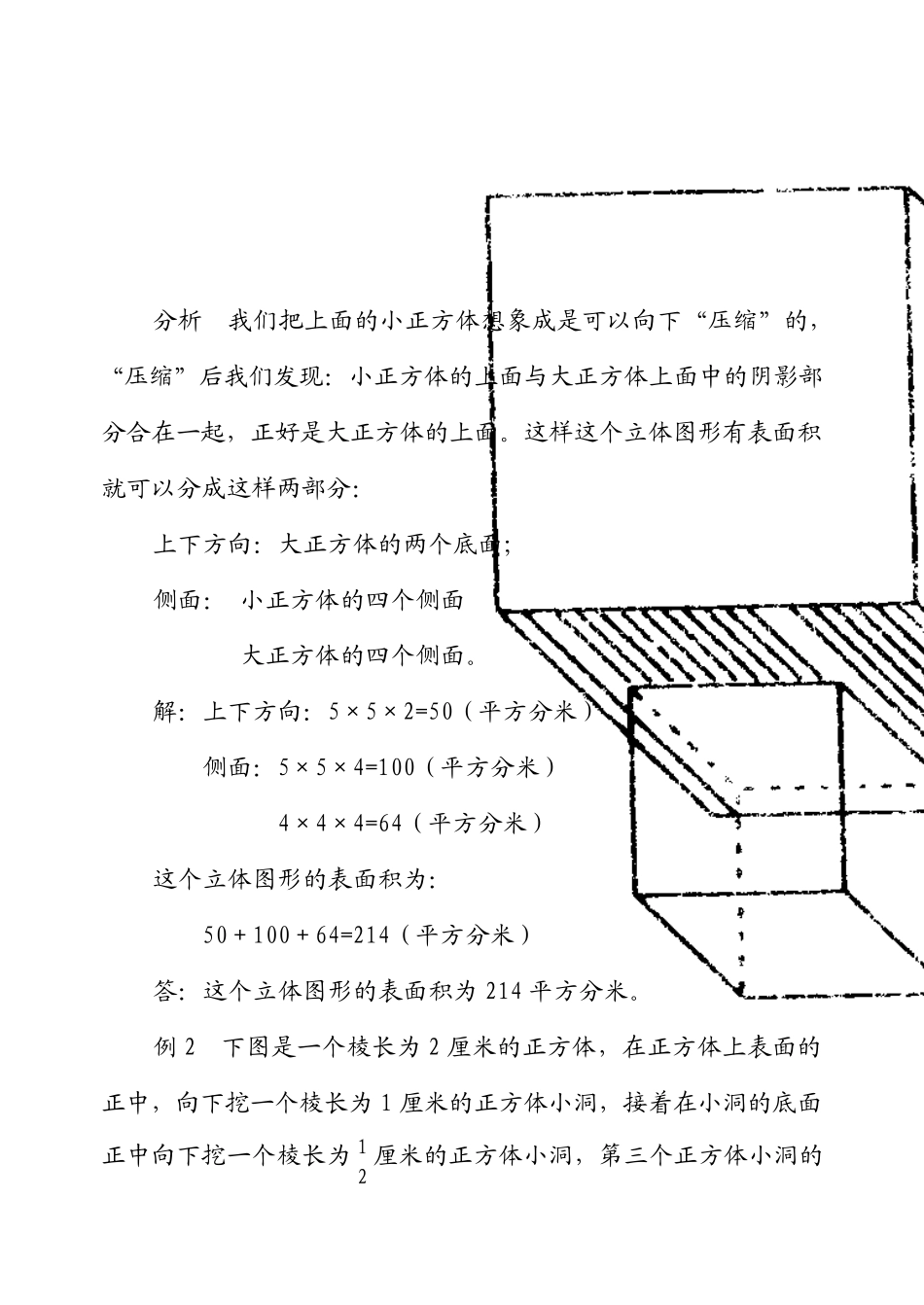
本系列共15 讲第三讲巧求表面积.文档贡献者:与你的缘我们已经学习了长方体和正方体,知道长方体或正方体六个面面积的总和叫做长方体或正方体的表面积。如果长方体的长用a 表示、宽用b 表示、高用h 表示,那么,长方体的表面积=(ab+ah+bh)×2。如果正方体的棱长用a 表示,则正方体的表面积=6a2。对于由几个长方体或正方体组合而成的几何体,或者是一个长方体或正方体组合而成的几何形体,它们的表面积又如何求呢?涉及立体图形的问题,往往可考查同学们的看图能力和空间想象能力。小学阶段遇到的立体图形主要是长方体和正方体,这些图形的特点都是可以从六个方向去看,特别是求表面积时,就是上下、左右和前后六个方向(有时只考虑上、左、前三个方向)的平面图形的面积的总和。有了这个原则,在解决类似问题时就十分方便了。例 1在一个棱长为 5 分米的正方体上放一个棱长为 4 分米的小正方体(下图),求这个立体图形的表面积。分析我们把上面的小正方体想象成是可以向下“压缩”的,“压缩”后我们发现:小正方体的上面与大正方体上面中的阴影部分合在一起,正好是大正方体的上面。这样这个立体图形有表面积就可以分成这样两部分:上下方向:大正方体的两个底面;侧面:小正方体的四个侧面大正方体的四个侧面。解:上下方向:5×5×2=50(平方分米)侧面:5×5×4=100(平方分米)4×4×4=64(平方分米)这个立体图形的表面积为:50+100+64=214(平方分米)答:这个立体图形的表面积为 214 平方分米。例 2下图是一个棱长为 2 厘米的正方体,在正方体上表面的正中,向下挖一个棱长为 1 厘米的正方体小洞,接着在小洞的底面正中向下挖一个棱长为厘米的正方体小洞,第三个正方体小洞的12挖法与前两个相同,棱长为厘米。那么最后得到的立体图形的表14面积是多少平方厘米?分析这道题的难点是洞里的表面积不易求。在小洞里,平行于上下表面的所有面的面积和等于边长为1 厘米的正方形的面积,这个边长为1厘米的正方形再与图中阴影部分的面积合在一起正好是边长为2 厘米的正方体的上表面的面积。这个立体图形的表面积分成两部分:上下方向:2 个边长为2 厘米的正方形的面积;边长为2 厘米的 4 个正方形的面积和侧面: 边长为1 厘米的 4 个正方形的面积和边长为厘米的 4 个正方形的面积和12边长为厘米的 4 个正方形的面积和14解:平行于上下表面的各面面积之和:2×2×2=8(平方厘米)侧面:2×2×4=16(平方厘米...