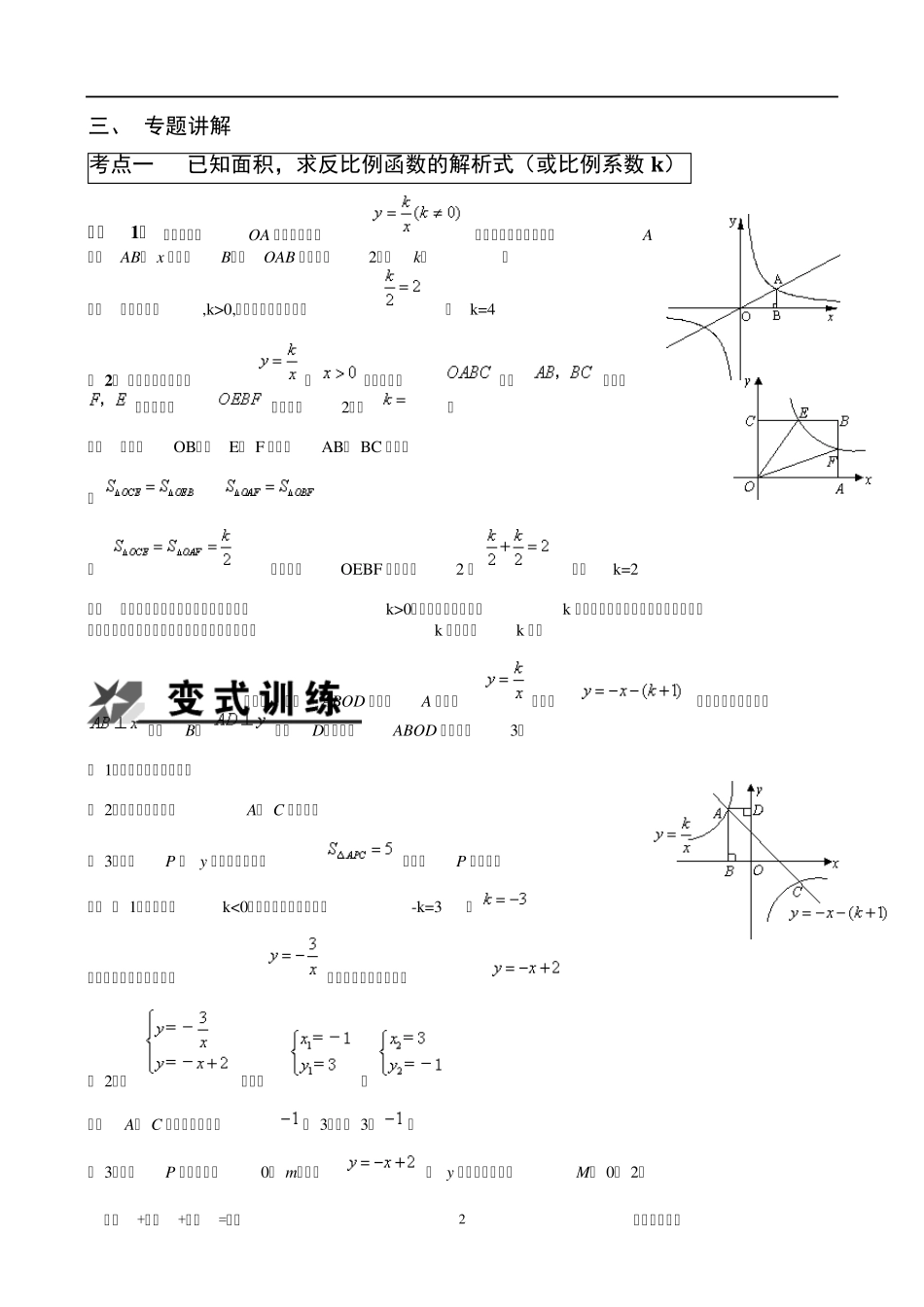
努力+勤奋+信心=成功 戴氏教育集团 1 DSE 金牌数学专题系列 经典专题系列第 1 讲 反比例函数中的面积问题 一、 导入: 《飞翔的蜘蛛》 信念是一种无坚不催的力量,当你坚信自己能成功时,你必能成功。 一天,我发现,一只黑蜘蛛在后院的两檐之间结了一张很大的网。难道蜘蛛会飞?要不,从这个檐头到那个檐头,中间有一丈余宽,第一根线是怎么拉过去的?后来,我发现蜘蛛走了许多弯路--从一个檐头起,打结,顺墙而下,一步一步向前爬,小心翼翼,翘起尾部,不让丝沾到地面的沙石或别的物体上,走过空地,再爬上对面的檐头,高度差不多了,再把丝收紧,以后也是如此。 温馨提示:蜘蛛不会飞翔,但它能够把网凌结在半空中。它是勤奋、敏感、沉默而坚韧的昆虫,它的网制得精巧而规矩,八卦形地张开,仿佛得到神助。这样的成绩,使人不由想起那些沉默寡言的人和一些深藏不露的智者。于是,我记住了蜘蛛不会飞翔,但它照样把网结在空中。奇迹是执着者造成的。 二、 知识点回顾 由于反比例函数解析式及图象的特殊性,很多中考试题都将反比例函数与面积结合起来进行考察。这种考察方式既能考查函数、反比例函数本身的基础知识内容,又能充分体现数形结合的思想方法,考查的题型广泛,考查方法灵活,可以较好地将知识与能力融合在一起。下面就反比例函数中与面积有关的问题的四种类型归纳如下: 利用反比例函数中|k|的几何意义求解与面积有关的问题 设 P 为双曲线上任意一点,过点P 作 x 轴、y 轴的垂线PM、 PN,垂足分别为M、 N,则两垂线段与坐标轴所围成的的矩形PMON 的面积为S=|PM|× |PN|=|y|× |x|=|xy| ∴ xy=k 故 S=|k| 从而得 结论1:过双曲线上任意一点作x 轴、y 轴的垂线,所得矩形的面积S 为定值|k| 对于下列三个图形中的情形,利用三角形面积的计算方法和图形的对称性以及上述结论,可得出对应的面积的结论为: 结论2: 在直角三角形ABO 中,面积S= 结论3:在直角三角形ACB 中,面积为S=2|k| 结论4:在三角形AMB 中,面积为S=|k| 努力+勤奋+信心=成功 戴氏教育集团 2 三、 专题讲解 考点一 已知面积,求反比例函数的解析式(或比例系数 k ) 【例1】 如图,直线OA 与反比例函数的图象在第一象限交于A点,AB⊥ x轴于点B,△OAB 的面积为2,则k= . 分析:由图象知,k>0,由结论及已知条件得 ∴ k=4 ( 2) 如图,已知双曲线()经过矩形的边的中点,且四边形的面积为2,则...