反比例函数的应用六种题型

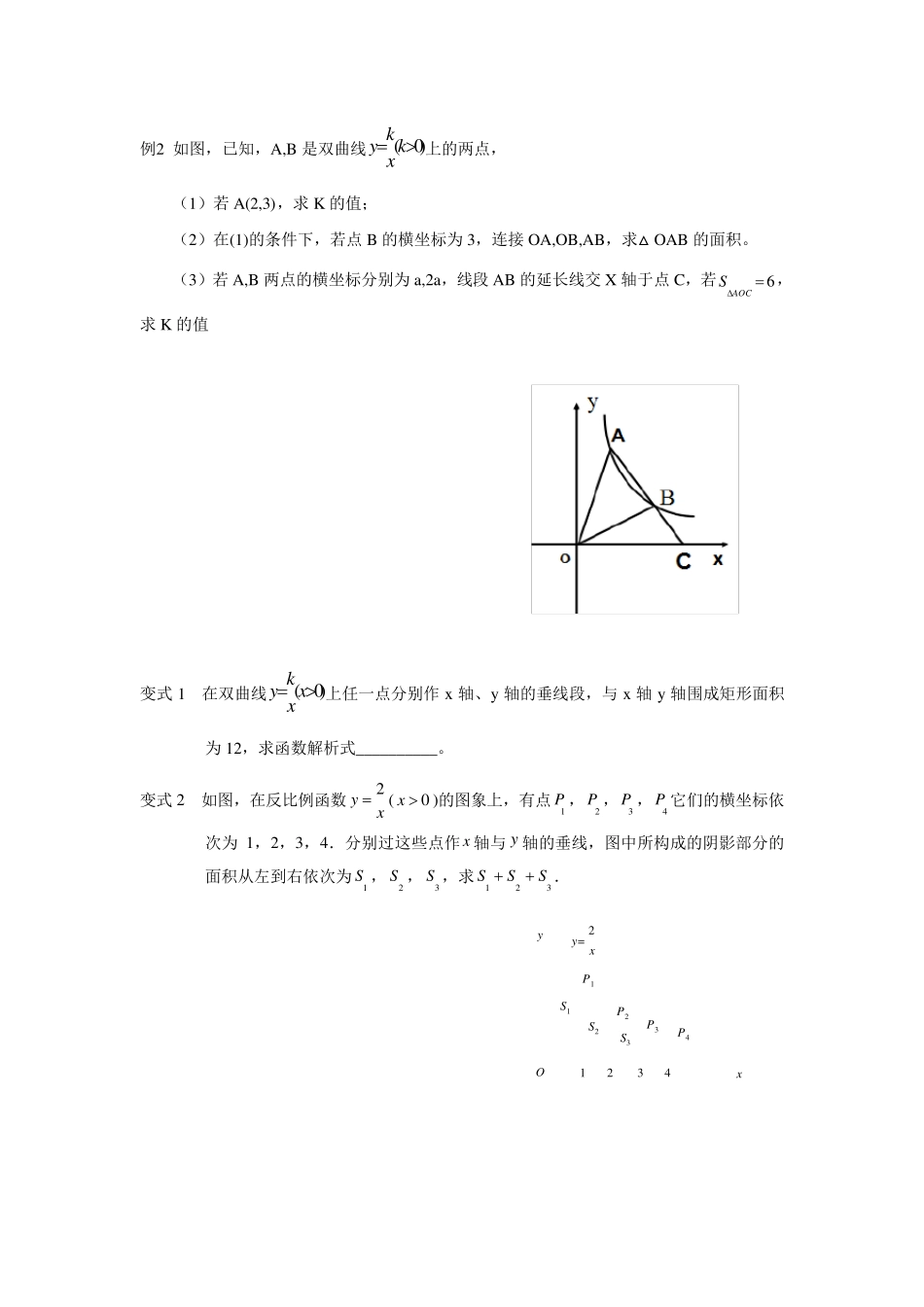
反比例函数实际应用的六种题型 题型一：在面积中的应用 一：面积不变性（k 的几何意义） 如图，设点P（a，b）是反比例函数y= xk上任意一点，作PA⊥x轴于 A 点，PB⊥y 轴于 B 点，则矩形 PBOA 的面积是k （三角形 PAO和三角形 PBO 的面积都是k21；面积是正数，所以 k 要加绝对值） S矩形 PBOA= k ； S三角形 PAO=S三角形 PBO=k21 注意： （1）面积与 P 的位置无关，即(0)kykx的面积不变性 （2）当 k 符号不确定的情况下须分类讨论 S△ABC=︱K︱； SABCD=2︱K︱ 二、曲直结合（一次函数与反比例函数） 典型例题 例1 如图,点P 是反比例函数xy2图象上的一点,PD⊥x 轴于 D.则△POD的面积为 . 例2 如图，已知，A,B 是双曲线 )0(  kxky上的两点， （1）若A(2,3)，求K 的值； （2）在(1)的条件下，若点B 的横坐标为3，连接OA,OB,AB，求△OAB 的面积。 （3）若A,B 两点的横坐标分别为a,2a，线段AB 的延长线交X 轴于点C，若6AOCS，求K 的值 变式1 在双曲线 )0(  xxky上任一点分别作x 轴、y 轴的垂线段，与 x 轴y 轴围成矩形面积为12，求函数解析式__________。 变式2 如图，在反比例函数2yx(0x )的图象上，有点1P ，2P ，3P ，4P 它们的横坐标依次为1，2，3，4．分别过这些点作x 轴与 y 轴的垂线，图中所构成的阴影部分的面积从左到右依次为1S ，2S ，3S ，求123SSS． S3S2S11 2 3 4y=2xP4P3P2xyOP1 变式3 如图，点P，Q 是反比例函数y= 图象上的两点，PA⊥y轴于点A，QN⊥x轴于点N，作 PM⊥x轴于点M，QB⊥y轴于点B，连接 PB、QM，△ABP 的面积记为 S1 ， △QMN 的面积记为 S2 ， 则 S1________S2 ． （填“＞” 或“＜” 或“=” ） 变式4 已知 ABCDE，，，，是反比例函数16yx0x图象上五个整数点（横、纵坐标均为整数），分别以这些点向横轴或纵轴作垂线段，由垂线段所在的正方形边长为半径作四分之一圆周的两条弧，组成如图5 所示的五个橄榄形，则这五个橄榄形的面积总和是__________（用含 π 的代数式表示） 变式5 如图正方形 OABC 的面积为 4，点O 为坐标原点，点B 在函数kyx(0,0)kx 的图象上，点P(m，n)是函数kyx(0,0)kx的图象上异于 B 的任意一点，过点P 分别作 x轴、y轴的垂线，垂足分别为 E、F． (1)设矩形 OEPF 的面积为 Sl，判断 Sl 与点P 的位置是否有关(不...