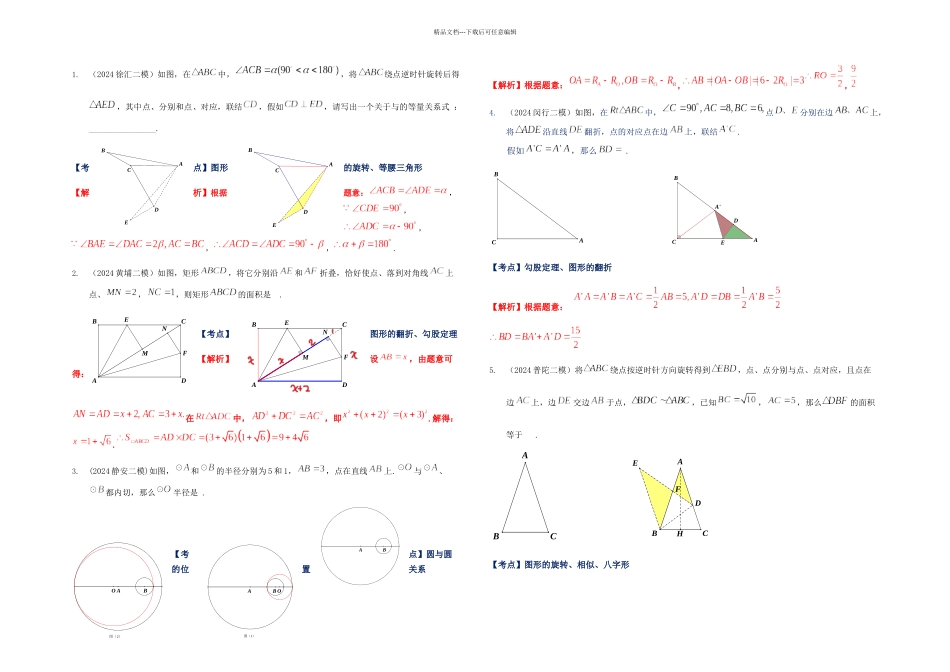
精品文档---下载后可任意编辑1.(2024 徐汇二模)如图,在中,,将绕点逆时针旋转后得,其中点、分别和点、对应,联结,假如,请写出一个关于与的等量关系式 :________________.【考点】图形的旋转、等腰三角形【解析】根据题意:,,,,,.2.(2024 黄埔二模)如图,矩形,将它分别沿和折叠,恰好使点、落到对角线上点、,,则矩形的面积是 . 【考点】图形的翻折、勾股定理【解析】设,由题意可得:在中,,即.解得:.3.(2024 静安二模)如图,和的半径分别为 5 和 1,,点在直线上.与、都内切,那么半径是 .【考点】圆与圆的位置关系【解析】根据题意:,,4.(2024 闵行二模)如图,在中,点分别在边上,将沿直线翻折,点的对应点在边上,联结.假如,那么 .【考点】勾股定理、图形的翻折【解析】根据题意: 5.(2024 普陀二模)将绕点按逆时针方向旋转得到,点、点分别与点、点对应,且点在边上,边交边于点,,已知,,那么的面积等于 .【考点】图形的旋转、相似、八字形EDCABEDCABNMFECBADNMFECBADBA图(1)BAO图(2)BAOEDA'BACHFEDACBBACACB精品文档---下载后可任意编辑【解析】6.(2024 杨浦二模)如图,在中,将翻折,是得点与点的中点重合,假如折痕与边的交点为,那么的长为 .【考点】图形的翻折、勾股定理、等腰直角三角【解析】过点作,设,根据题意得:,在中,7.(2024 嘉定二模)如图,在中,,将绕着点旋转,点、的对应点分别记为、,与边相交于点,假如那么线段的长为 . 【考点】图形的旋转、母子三角形、锐角三角比【解析】根据题意:,,8.(2024 长宁、金山、青浦二模)如图,在中,是斜边上两点,,将绕点顺时针旋转后,得到.设.那么 .【考点】图形的翻折、勾股定理【解析】将沿翻折得到,联结.根据题意得:,.9.(2024 崇明二模)如图,已知中,平分,将绕着点旋转后,点、的对应点分别记为,假如点落在射线的长度为.【考点】图形的旋转、八字形、旋转相似【解析】,即10. (2024 虹口二模)如图,在中,点在斜边上,把沿直线翻折,使得点落在同一平面内的处,当平行的直角边时,的长为 .HFEMBCAABCEA'B'FABCECABDECABDFC1B1DBACDBAC321EA'DACB312A'DACBACBBCA精品文档---下载后可任意编辑【考点】图形的翻折、八字形【解析】图(2)根据题意图(3)根据题意.综上:或.11. (2024 松江二模)如图,已知在矩形中,,将沿对角线翻折,点落在点处,联结,则的长为 .【考点】图形的翻折、八字形、勾股...