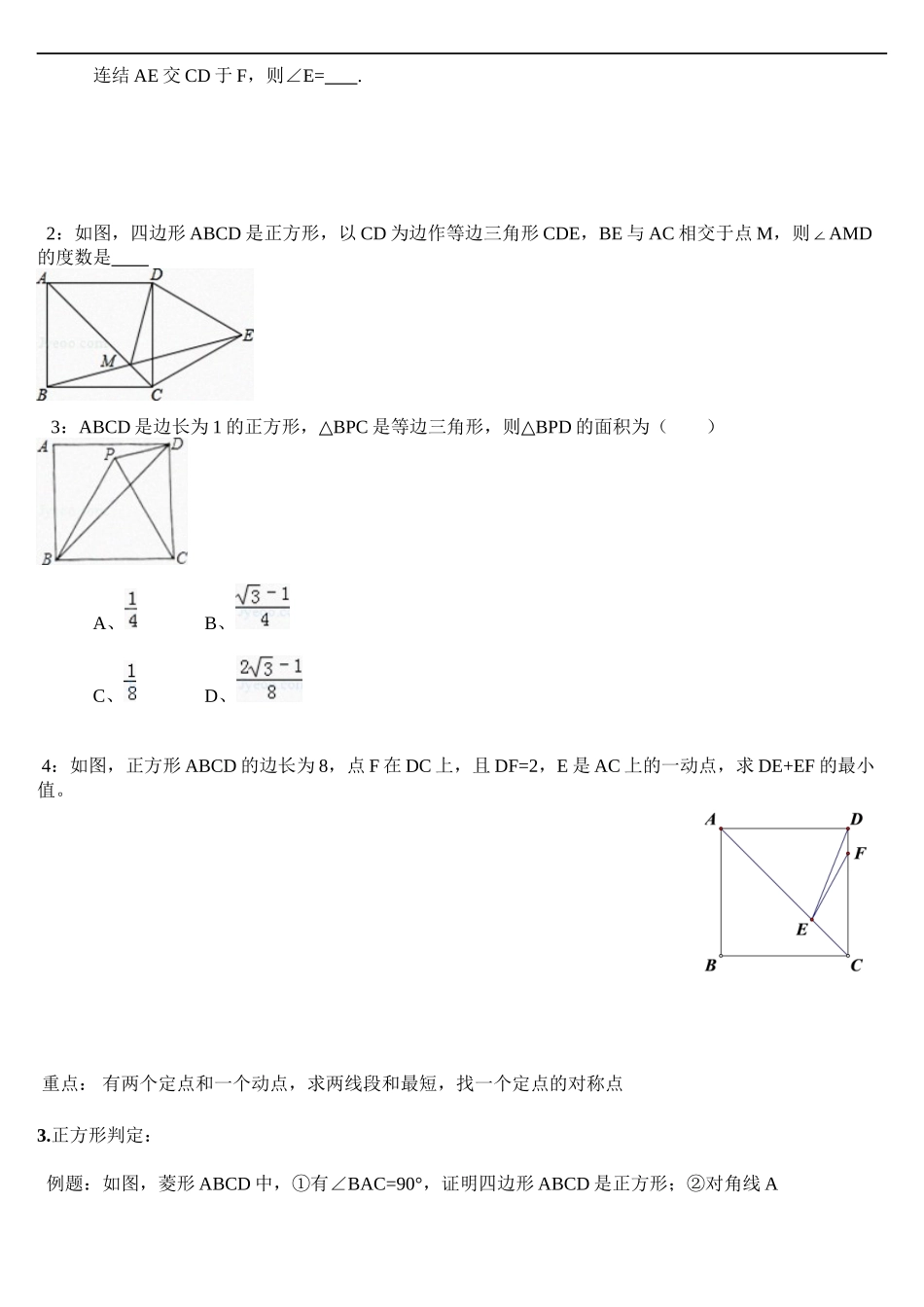
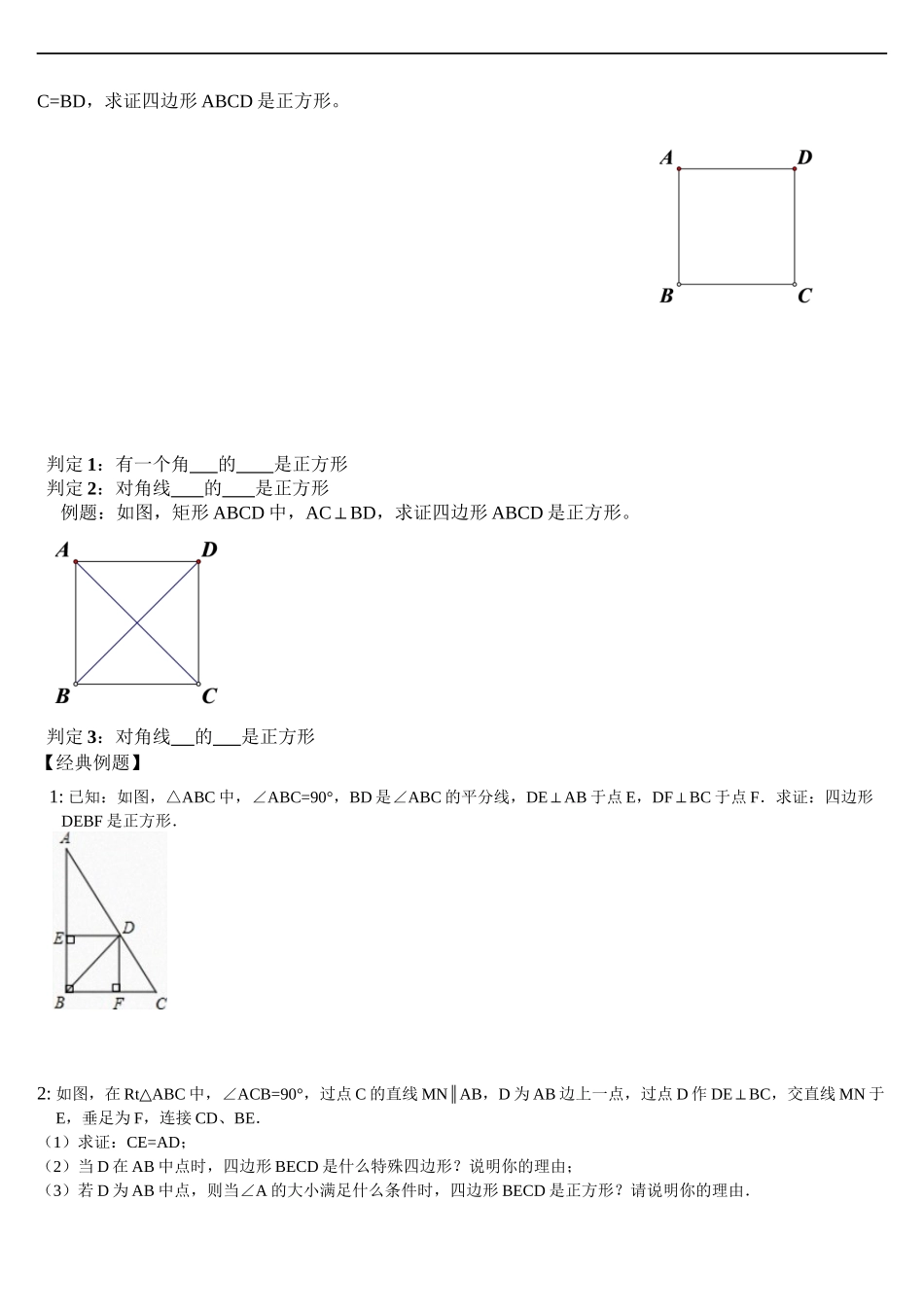
ADECBF 正方形的性质与判断一. 目标1.经历探索、猜想、证明的过程,进一步发展推理论证的能力。2.能运用综合法证明矩形的判定定理。3.感悟在证明过程中所运用的归纳、类比、转化等思想方法。二.学习重点掌握正方行的性质和判定以及证明方法。三.知识回顾 1.平行四边形定义:两组对边 ,叫平行四边形。 2. 平行四边形性质: , , . 3. 平行四边形判定: , , 。 4 菱形的性质: , 。 5. 菱形的判定: , , 。 6.矩形的性质: , 。 7. 矩形形的判定: , , 。 四.课程重点 知识点二:正方形1.定义:有一组邻边 ,且有一个 的 叫做正方形。菱形,矩形,正方形和平行四边形的关系?2.性质: 定理:正方形 ABCD 中,四个角和四条边的关系,两条对角线关系? 性质 1:正方形的四个角都是 ,四条边都 。 性质 2:正方形的对角线 且 。【经典例题】 1:、如图,在正方形 ABCD 的边 BC 的延长线上取一点 E,使 CE=AC, 连结 AE 交 CD 于 F,则∠E= . 2:如图,四边形 ABCD 是正方形,以 CD 为边作等边三角形 CDE,BE 与 AC 相交于点 M,则∠AMD的度数是 3:ABCD 是边长为 1 的正方形,△BPC 是等边三角形,则△BPD 的面积为()A、B、C、D、 4:如图,正方形 ABCD 的边长为 8,点 F 在 DC 上,且 DF=2,E 是 AC 上的一动点,求 DE+EF 的最小值。 重点 : 有两个定点和一个动点,求两线段和最短,找一个定点的对称点3.正方形判定: 例题:如图,菱形 ABCD 中,①有∠BAC=90°,证明四边形 ABCD 是正方形;②对角线 A C=BD,求证四边形 ABCD 是正方形。 判定 1:有一个角 的 是正方形 判定 2:对角线 的 是正方形 例题:如图,矩形 ABCD 中,ACBD⊥,求证四边形 ABCD 是正方形。 判定 3:对角线 的 是正方形【经典例题】 1: 已知:如图,△ABC 中,∠ABC=90°,BD 是∠ABC 的平分线,DEAB⊥于点 E,DFBC⊥于点 F.求证:四边形DEBF 是正方形.2: 如图,在 Rt ABC△中,∠ACB=90°,过点 C 的直线 MN AB∥,D 为 AB 边上一点,过点 D 作 DEBC⊥,交直线 MN 于E,垂足为 F,连接 CD、BE.(1)求证:CE=AD;(2)当 D 在 AB 中点时,四边形 BECD 是什么特殊四边形?说明你的理由;(3)若 D 为 AB 中点,则当∠A 的大小满足什么条件时,四边形 BECD 是正方形?请说明你的理由....