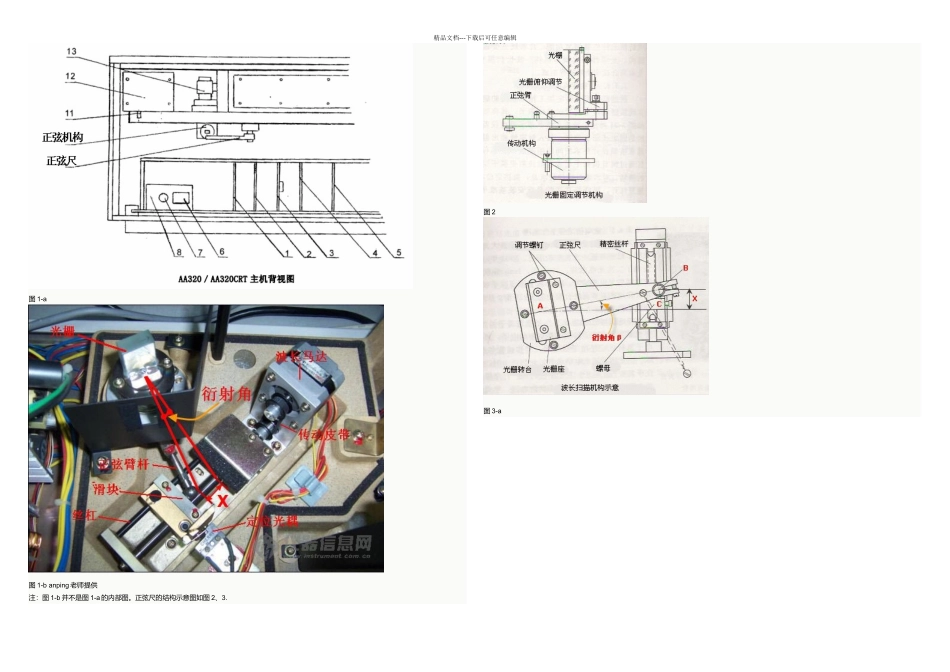
精品文档---下载后可任意编辑图 1-a 图 1-b anping 老师提供注:图 1-b 并不是图 1-a 的内部图。正弦尺的结构示意图如图 2、3.图 2图 3-a精品文档---下载后可任意编辑 图 3-b anping 老师提供(三)正弦机构的工作原理 如图 3-a,光栅平面转动中心与一被称为正弦尺的金属杆的 A 端连接,杆的 B 端装有滚动轴承, 正弦尺的 A 点到 B 点距离,即光栅平面转动中心与轴承转动中心间距离,设为 L。滚动轴承靠近丝母 C 的端面,当精密丝杆转动时,使螺母沿丝杆移动,X 值(丝母沿丝杆移动的距离)变化,最终推动正弦杆带着光栅绕其中心轴转动,从而 AB 线和 CA 线间的夹角即光栅的衍射角 β 随之改变。以图 1-b 为例来说明:波长马达通过传动皮带驱动精密丝杆转动,丝杆带动滑块移动,由于正弦臂杆是靠在滑块上的,所以正弦臂杆也跟着转动,从而带动光栅转动。 (四)波长的线性化 图 3-a 的简化图如图 4。为了便于说明,以下的说明基于李特洛型光栅单色器或者闪耀光栅。图 4 光栅型单色器依据的原理是光栅方程 mλ=d(sinα+sinβ)。 光栅方程 mλ=d(sinα+sinβ) m 为光谱级次,λ 为衍射光波长,d 光栅常数,α 为入射角,β 为衍射角。 入射角 α 和衍射角 β 的正负号规定为:衍射光和入射光在法线的同一侧时,入射角和衍射角同号,否则异号。 m=0 为零级光,零级光两侧均有光谱,m>0 的为正级光谱,m<0 的为负级光谱。光栅方程 mλ=d(sinα+sinβ),可以写成 mλ = 2 * d * sin[(α+β)/2] * cos[(α-β)/2] 式 1-1 设计单色器系统以使上式简化,对于正弦机构,设计机构,使 (α-β)为一常数。 对于李特洛型光栅单色器或者闪耀光栅,衍射角 β 和入射角 α 相等,即 α=β。图 5 式 1-1 简化为: mλ=2d(sinβ) 式 1-2 根据图 4 可以看出, sinβ = X / L 式 1-3 得 mλ = 2d(X/L) 式 1-4 对于一定的光谱级次 m 和固定的正弦杆长度 L;对于固定的光栅,d 固定。 可以看到 λ = KX 式 1-5 衍射波长 λ 和丝母沿丝杆移动的距离 X 成正比。这意味着波长随丝杆转动而线性变化,从而使波长读数值呈线性变化成为可能,如图周,波长被线性化了。 现代仪器一般采纳精密步进电机驱动丝杆,如图 1-b,步进电机转动的角度由微处理器计算,这样也就可以算出相应的波长。 参考文献:1. 原子吸收光谱仪 章诒学 何...