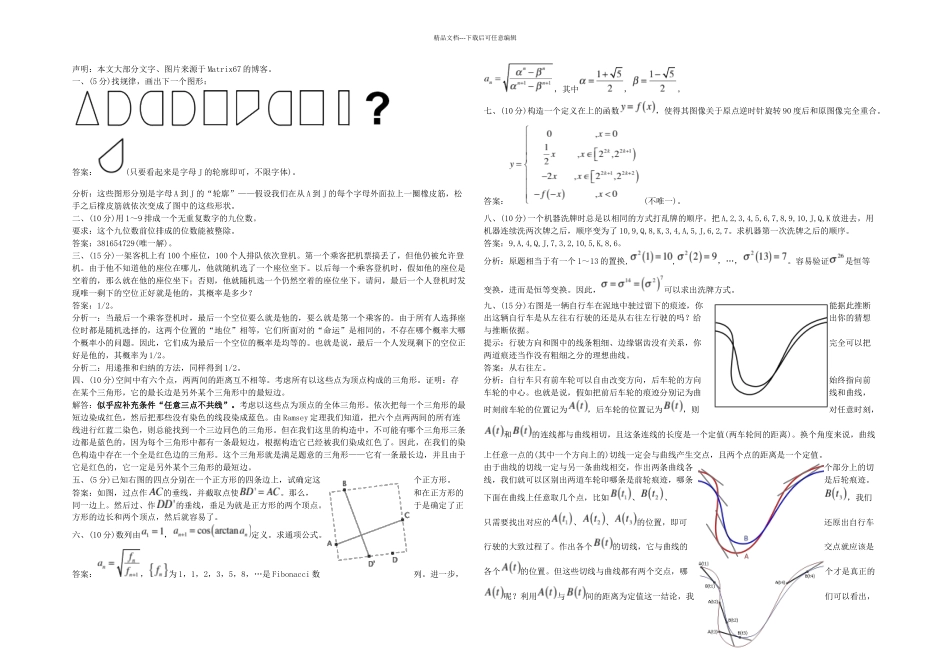
精品文档---下载后可任意编辑声明:本文大部分文字、图片来源于 Matrix67 的博客。一、(5 分)找规律,画出下一个图形:答案:(只要看起来是字母 J 的轮廓即可,不限字体)。分析:这些图形分别是字母 A 到 J 的“轮廓”——假设我们在从 A 到 J 的每个字母外面拉上一圈橡皮筋,松手之后橡皮筋就依次变成了图中的这些形状。二、(10 分)用 1~9 排成一个无重复数字的九位数。要求:这个九位数前位排成的位数能被整除。答案:381654729(唯一解)。三、(15 分)一架客机上有 100 个座位,100 个人排队依次登机。第一个乘客把机票搞丢了,但他仍被允许登机。由于他不知道他的座位在哪儿,他就随机选了一个座位坐下。以后每一个乘客登机时,假如他的座位是空着的,那么就在他的座位坐下;否则,他就随机选一个仍然空着的座位坐下。请问,最后一个人登机时发现唯一剩下的空位正好就是他的,其概率是多少?答案:1/2。分析一:当最后一个乘客登机时,最后一个空位要么就是他的,要么就是第一个乘客的。由于所有人选择座位时都是随机选择的,这两个位置的“地位”相等,它们所面对的“命运”是相同的,不存在哪个概率大哪个概率小的问题。因此,它们成为最后一个空位的概率是均等的。也就是说,最后一个人发现剩下的空位正好是他的,其概率为 1/2。分析二:用递推和归纳的方法,同样得到 1/2。四、(10 分)空间中有六个点,两两间的距离互不相等。考虑所有以这些点为顶点构成的三角形。证明:存在某个三角形,它的最长边是另外某个三角形中的最短边。解答:似乎应补充条件“任意三点不共线”。考虑以这些点为顶点的全体三角形。依次把每一个三角形的最短边染成红色,然后把那些没有染色的线段染成蓝色。由 Ramsey 定理我们知道,把六个点两两间的所有连线进行红蓝二染色,则总能找到一个三边同色的三角形。但在我们这里的构造中,不可能有哪个三角形三条边都是蓝色的,因为每个三角形中都有一条最短边,根据构造它已经被我们染成红色了。因此,在我们的染色构造中存在一个全是红色边的三角形。这个三角形就是满足题意的三角形——它有一条最长边,并且由于它是红色的,它一定是另外某个三角形的最短边。五、(5 分)已知右图的四点分别在一个正方形的四条边上,试确定这个正方形。答案:如图,过点作的垂线,并截取点使。那么,和在正方形的同一边上。然后过、作的垂线,垂足为就是正方形的两个顶点。于是确定了正方形的边长和两个顶点...